Подграфы и части графа

Пусть G (V, E) – исходный граф (рис. 2.9).

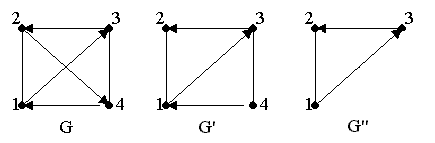
Рисунок 2.9

G ’(V ’, E ’) – часть графа – это могут быть все вершины, но дуги не все.

V ’ 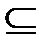V, E ’ 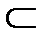E (V ’ V ’).

Если у части графа V ’ = V, то ее называют суграфом.

G ”(V ”, E ”) – подграф – часть графа, в которой сохранены все ребра, связывающие вершины графа V ” 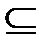V, E ” = Е (V ” V ”).

Гомоморфизм и изоморфизм графов. Пусть имеем граф G (V, E) (рис. 2.10). И пусть имеется отображение: j: V ® V ¢, при котором

[ a, b ], a, b Î V Þ [j (a), j (b)], j (a), j (b) Î V ¢.

Такое отображение называется гомоморфизмом.

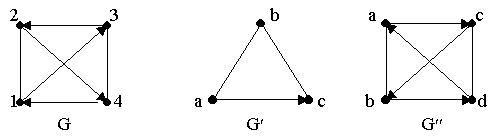
Рисунок 2.10

Если отображение взаимно однозначно: y: V «V ¢, то это изоморфизм.

Изоморфные графы эквивалентны с точность до обозначений вершин.