2015-05-14
6089
Для дифференциального уравнения 2-го порядка (при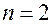 
) начальные условия (2) имеют вид тройки чисел 
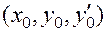, и ставится задача отыскания решения 
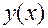, для которого 
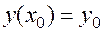и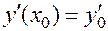 
. Геометрически это означает выбор из совокупности интегральных кривых той, которая, во-первых, проходит через заданную точку плоскости 
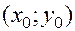, и, во-вторых, имеет в этой точке заданный угловой коэффициент касательной 
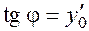(рис. 2).
 |
Рис. 2
