Рассмотрим показательную функцию
y(x) = ax
В дальнейшем будем считать, что основание степени a является положительным числом:
a > 0.
Тогда функция y = ax определена для всех x. Ее область определения:
- ∞ < x + ∞.
При a ≠ 1 она имеет множество значений:
0 < y < + ∞
При a = 1 показательная функция является постоянной
y = 1
24 Криволине́йная трапе́ция — плоская фигура, ограниченная графиком неотрицательной непрерывной функции 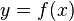 , определенной наотрезке [a; b], осью абсцисс и прямыми
, определенной наотрезке [a; b], осью абсцисс и прямыми  и
и  .
.
Для нахождения площади криволинейной трапеции пользуются интегралом.
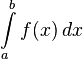
Или
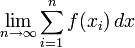
Это значит, что площадь криволинейной трапеции можно найти по сумме значений функции 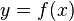 взятые через бесконечно малые промежутки по оси Ох наотрезке от
взятые через бесконечно малые промежутки по оси Ох наотрезке от 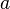 до
до 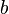
Можно сказать, что мы разбили криволинейную трапецию на бесконечное число прямоугольников, длина каждого из которых равна ординате функции 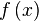 через бесконечно малые промежутки по оси Ох на отрезке от
через бесконечно малые промежутки по оси Ох на отрезке от 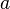 до
до 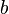 , а ширина — бесконечно малому значению х, нашли их площади произведением длины на ширину и сложили. Предел суммы их площадей равен площади криволинейной трапеции.
, а ширина — бесконечно малому значению х, нашли их площади произведением длины на ширину и сложили. Предел суммы их площадей равен площади криволинейной трапеции.
25 Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
26 Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием интеграла Римана и вычислениемпервообразной.
Если 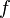 непрерывна на отрезке непрерывна на отрезке 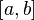 и и 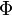 — её любая первообразная на этом отрезке, то имеет место равенство — её любая первообразная на этом отрезке, то имеет место равенство 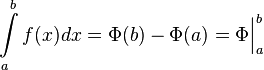 |
· 27 Степенна́я фу́нкция — функция 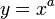 , где
, где 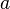 (показатель степени) — некоторое вещественное число[1]. К степенным часто относят и функцию вида
(показатель степени) — некоторое вещественное число[1]. К степенным часто относят и функцию вида 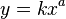 , где k — некоторый масштабный множитель.[2] Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда являетсяцелым или рациональным числом. Графики степенной функции при натуральном показателе n называются параболами порядка n. При
, где k — некоторый масштабный множитель.[2] Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда являетсяцелым или рациональным числом. Графики степенной функции при натуральном показателе n называются параболами порядка n. При 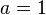 получается функция
получается функция 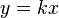 , называемая прямой пропорциональной зависимостью.
, называемая прямой пропорциональной зависимостью.
· Графики функций вида 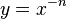 , где n — натуральное число, называются гиперболами порядка n. При
, где n — натуральное число, называются гиперболами порядка n. При 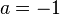 получается функция
получается функция 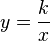 , называемая обратной пропорциональной зависимостью.
, называемая обратной пропорциональной зависимостью.
· Если 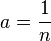 , то функция есть арифметический корень степени n.
, то функция есть арифметический корень степени n.
28 Первообрáзной [1] или примити́вной функцией (иногда называют также антипроизводной) данной функции 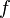 называют такую
называют такую 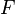 , производная которой (на всей области определения) равна
, производная которой (на всей области определения) равна 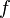 , то есть
, то есть 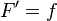 . Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Так, например, функция  является первообразной
является первообразной 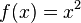 . Так как производная константы равна нулю,
. Так как производная константы равна нулю, 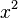 будет иметь бесконечное количество первообразных, таких как
будет иметь бесконечное количество первообразных, таких как 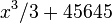 или
или 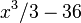 и т. д.; таким образом, семейство первообразных функции
и т. д.; таким образом, семейство первообразных функции 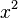 можно обозначить как
можно обозначить как 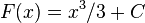 , где
, где 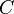 — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения
— любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения 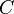 .
.
Первообразные важны тем, что позволяют вычислять интегралы. Если 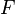 — первообразная интегрируемой функции
— первообразная интегрируемой функции 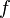 , то:
, то:
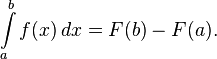
29·
Зафиксировать значение x, найти f(x).
· Дать аргументу x приращение Dx, перейти x+Dx в новую точку, найти f(x+Dx).
· Найти приращение функции: Dy= f(x+Dx)-f(x)
· Составить отношение
· Вычислить предел (этот предел и есть f `(x).)
Примеры:
Пример 1.: Найти производную постоянной функции у=С
Решение: Воспользуемся алгоритмом отыскания производной.
- Для фиксированного значения х имеем f(x)=С.
- В точке f(x+Dx)=С.
- Dу=С - С=0.
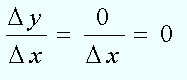
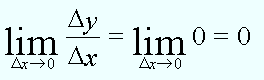 Ответ: (С)'=0
Ответ: (С)'=0
30На предыдущих занятиях были рассмотрены задачи на технику дифференцирования. Это очень важные задачи, и нахождение производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.
Построим кривую 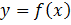 (см. рис.1).
(см. рис.1).
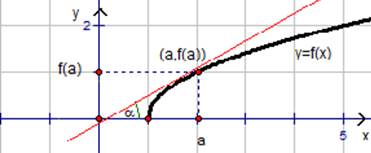
Рис. 1. График функции 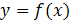 .
.
Зафиксируем точку 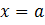 . Если
. Если 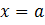 , то значение функции равно
, то значение функции равно 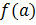 . Значит, имеем точку с координатами (
. Значит, имеем точку с координатами (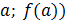 .
.
Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции 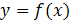 в точке с абсциссой
в точке с абсциссой 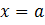 , в которой
, в которой 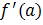 - существует.
- существует.
Уравнение касательной – это прямая, которая задается формулой 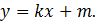
Любая прямая, в том числе и касательная, определяется двумя числами: 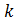 и
и 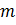 . Исходя из геометрического смысла производной
. Исходя из геометрического смысла производной 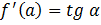 (тангенс угла наклона касательной) – это есть угловой коэффициент
(тангенс угла наклона касательной) – это есть угловой коэффициент 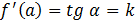 .
.
Параметр 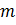 найдем из условия, что касательная проходит через точку (
найдем из условия, что касательная проходит через точку (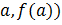 , то есть
, то есть 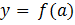 .
.
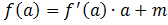 .
.
Стало быть 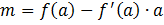 .
.
Запишем уравнение касательной
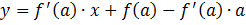 .
.
Или, 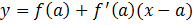 .
.
Получили уравнение касательной к кривой 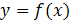 в точке с абсциссой
в точке с абсциссой 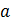 .
.
---31Показательные неравенства
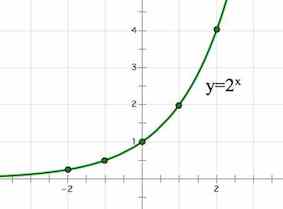 Сегодня решаем показательные неравенства.
Сегодня решаем показательные неравенства.
Рассмотрим основные типы показательных неравенств.
При решении показательных неравенств мы будем использовать следующие переходы:
и
Поясним, первый переход возникает в силу возрастания показательной функции, второй – в силу убывания функции.
 2015-05-14
2015-05-14 2211
2211
