(дополнительное рассмотрение)
Оценим разность 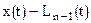 , где t – любое фиксированное значение в промежутке
, где t – любое фиксированное значение в промежутке 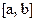 , отличное от узлов интерполирования (таблицы). Предположим, что функция
, отличное от узлов интерполирования (таблицы). Предположим, что функция 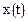 в этом промежутке имеет производные всех порядков до (n+1)-го включительно.
в этом промежутке имеет производные всех порядков до (n+1)-го включительно.
Введем в рассмотрение функцию 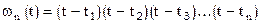 - полином степени n.
- полином степени n.
Построим вспомогательную функцию 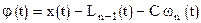 ,
,
где C – const. 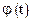 также имеет производные всех порядков до (n+1)-го включительно.
также имеет производные всех порядков до (n+1)-го включительно.
Значение константы С выберем так, чтобы для какого-либо аргумента 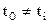
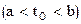 выполнялось
выполнялось 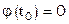 :
: 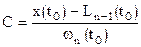 .
.
Поскольку 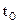 не совпадает ни с одни узлом, то
не совпадает ни с одни узлом, то 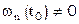 .
.
Вспомним теорему Ролля.
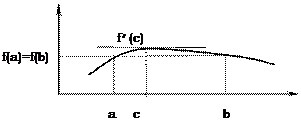 Если функция
Если функция 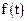 определена, непрерывна и дифференцируема на промежутке
определена, непрерывна и дифференцируема на промежутке 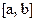 , а на концах промежутка функция принимает равные значения
, а на концах промежутка функция принимает равные значения 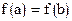 , то в промежутке
, то в промежутке 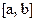 найдется такая точка с (a<c<b), что
найдется такая точка с (a<c<b), что 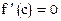 .
.
На промежутке 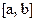 в точке
в точке 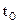 и в n узлах
и в n узлах 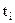 вспомогательная функция
вспомогательная функция 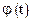 n+2 раза обращается в 0, то есть имеет n+1 корень. Эти корни делят промежуток
n+2 раза обращается в 0, то есть имеет n+1 корень. Эти корни делят промежуток 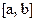 на n отрезков, на концах которых значения
на n отрезков, на концах которых значения 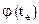 равны между собой (
равны между собой (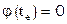 ). Согласно теореме Ролля на отрезке
). Согласно теореме Ролля на отрезке 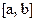 1-я производная
1-я производная 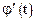 n раз обращается в 0, то есть имеет n корней. Эти корни делят промежуток
n раз обращается в 0, то есть имеет n корней. Эти корни делят промежуток 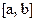 на n-1 отрезок, на концах которых значения
на n-1 отрезок, на концах которых значения 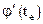 равны между собой (
равны между собой (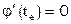 ). Поэтому, согласно теореме Ролля на отрезке
). Поэтому, согласно теореме Ролля на отрезке 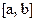 2-я производная
2-я производная 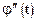 n-1 раз обращается в 0, то есть имеет n-1 корень. Эти корни делят промежуток
n-1 раз обращается в 0, то есть имеет n-1 корень. Эти корни делят промежуток 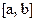 на n-2 отрезка, на концах которых значения
на n-2 отрезка, на концах которых значения 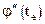 равны между собой (
равны между собой (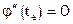 ). Поэтому, согласно теореме Ролля на отрезке
). Поэтому, согласно теореме Ролля на отрезке 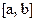 3-я производная
3-я производная 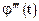 n-2 раза обращается в 0, то есть имеет n-2 корня.
n-2 раза обращается в 0, то есть имеет n-2 корня.
Продолжая, на n шаге получим один корень 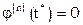 , где
, где 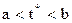 .
.
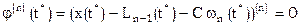
n производная 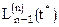 от полинома n-1 степени – ноль:
от полинома n-1 степени – ноль: 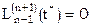 .
.
n производная 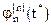 от полинома n степени, легко проверить:
от полинома n степени, легко проверить:
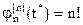 .
.
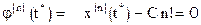 , откуда найдем
, откуда найдем
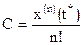 .
.
Вернемся к точке 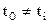 :
: 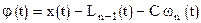 ,
,
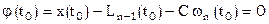 ,
,
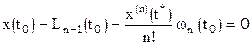 ,
,
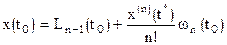 или, поскольку принимает произвольное значение
или, поскольку принимает произвольное значение 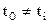 ,
, 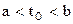 , перейдем к аргументу t
, перейдем к аргументу t
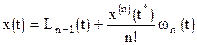 ,
, 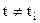 . [9]
. [9]
Это точное равенство – интерполяционная формула Лагранжа, здесь 2-е слагаемое и есть искомый остаточный член. Оценим его величину.
Пусть число 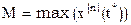 на отрезке
на отрезке 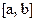 . Поскольку
. Поскольку
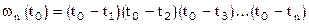 , а
, а 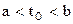 , то
, то 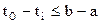 ,
,
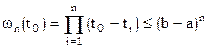 . Отсюда следует, что величина остаточного члена
. Отсюда следует, что величина остаточного члена
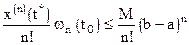 .
.
 2015-05-14
2015-05-14 523
523








