Принцип Лежандра

Поскольку в системе [3] уравнений больше чем неизвестных, то не существует таких значений корней x₁, x₂, x₃,…x_n которые бы удовлетворяли одновременно всем уравнениям системы. Система [3] несовместна. Иными словами, подстановка любых значений неизвестных, например, 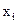даст

.

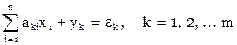Очевидно, естественно выбрать значения неизвестных 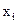так, чтобы модули невязок 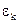были бы возможно меньшими.

Если дана система равноточных условных уравнений, то условимся искать неизвестные так, чтобы сумма квадратов невязок была наименьшей. Это и есть принцип Лежандра. Хотя нельзя обеспечить малость отдельных невязок, но минимальность суммы квадратов обеспечивает ограниченность и отдельных невязок. Иными словами, необходимо найти минимум аналитической функции – суммы квадратов невязок 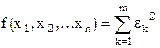. Необходимые условия минимума этой функции:

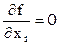
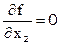[4]

… … …

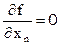
[4] – система нормальных уравнений. Для определения неизвестных всегда получается система с числом уравнений, равным числу неизвестных, поэтому задача становится определенной. Для 1-го уравнения системы [4]

,

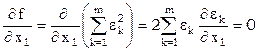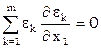, подставляя значение 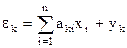, получим

,

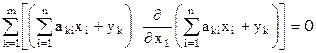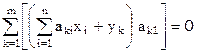, меняя порядок суммирования в первом слагаемом

.

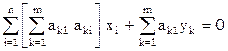Введем обозначения Гаусса 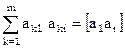, i=1,n,

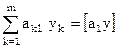, тогда последнее уравнение примет вид 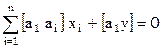или, в развернутом виде

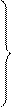
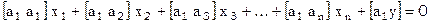
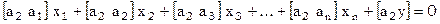
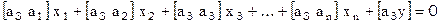[5]

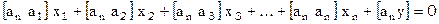
Решение системы нормальных уравнений [5] соответствует минимуму суммы квадратов невязок 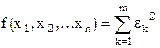, поэтому метод получил название метода наименьших квадратов.

Пример Таблично задана функция

x	y
1.4	5.1
2.3	4.2
3.4	3.3

Методом наименьших квадратов найти линейное уравнение, представляющее данные таблицы в виде .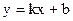

Здесь неизвестны коэффициенты k и b. Перепишем эту функцию в виде 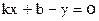. В предыдущих обозначениях с индексами это два неизвестных х₁ и х₂.

Составляем условные уравнения в виде

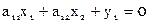
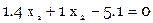
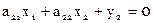
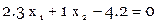
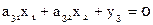
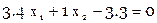
Расширенная матрица коэффициентов условных уравнений

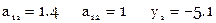
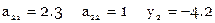
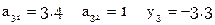
Расширенная матрица коэффициентов нормальных уравнений вычисляется так

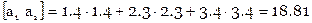
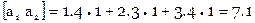
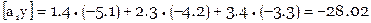
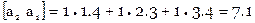
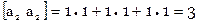
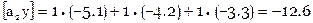
Итак

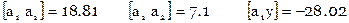
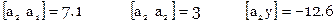
Система нормальных уравнений

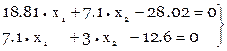, решая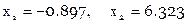

Возвращаясь к прежним обозначениям ,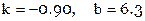

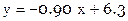
Найдем невязки 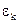(см. табличную функцию)

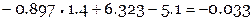
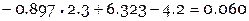
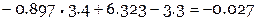
Отметим, что .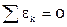

Пример Утром, после восхода Солнца, метеоролог отмечал рост температуры воздуха

время	температура
8h15m	17О
8h30m	18О
8h40m	19О

Найти формулу, позволяющую вычислить температуру, зная время на интервале с 8 до 9 часов утра в виде T= at+b.

Составляем условные уравнения, считая что время отсчитывается в минутах с 8 часов утра.

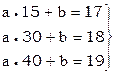
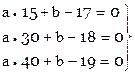
Расширенная матрица коэффициентов условных уравнений

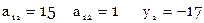
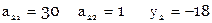
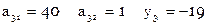
Расширенная матрица коэффициентов нормальных уравнений

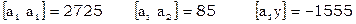
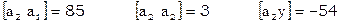
Система нормальных уравнений

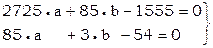, решая b=18-28.33 a

2725 a + 85 (18-28.33 a)-1555 = 0,

316.95 a – 25 = 0,

a = 0.0789,

b = 15.76,

Итак, T = 0.0789 t + 15.76

из формулы O-C

t = 15^m T=17^O T=16.94^O 0.06

t = 30^m T=18^O T=18.13^O -0.13

t = 40^m T=19^O T=18.92^O 0.08

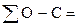0.01