Составление нормальных уравнений надо контролировать. В каждом условном уравнении образуем сумму sk коэффициентов при всех неизвестных и свободного члена; sk есть сумма элементов k–й строки расширенной матрицы коэффициентов.
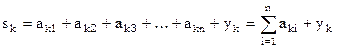
Далее вычисляем сумму произведений по столбцам системы условных уравнений и подставляем значение sk
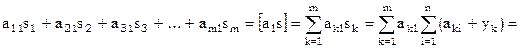
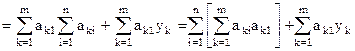
или в обозначениях Гаусса
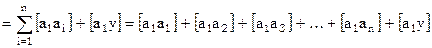 ,
,
а это сумма коэффициентов и свободного члена 1-го нормального уравнения!
Итак
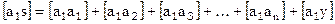
Для проверки составления нормальных уравнений следует проделать следующее:
1. просуммировать коэффициенты и свободный член каждого условного уравнения (найти sk)
2. найти сумму произведений коэффициентов 1-го столбца на суммы sk
3. найти суммы коэффициентов и свободного члена 1-го нормального уравнения
4. суммы, найденные в п.2 и п.3 должны совпадать.
Аналогично поступаем для проверки составления 2-го, 3-го и т.д. нормальных уравнений.

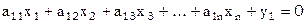 s1 m>n
s1 m>n
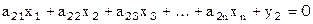 s2
s2
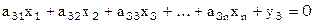 s3
s3
… … … … … …
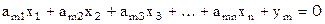 sm
sm
 |
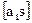
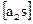
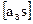
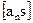

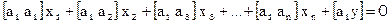
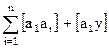
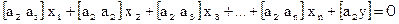
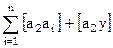
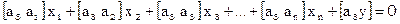
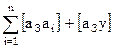
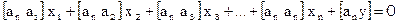
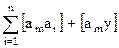
контроль k-й строки 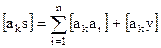
При умножениях и сложениях надо сохранять все знаки, какие формально получаются при действиях с приближенными числами. Тогда контрольные равенства должны удовлетворяться точно.
|
|
|
Пример Проведем контроль составления нормальных уравнений предыдущего примера.
условные уравнения s
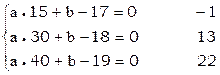
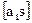
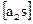
1255 34
нормальные уравнения (суммы коэфф и св члена)
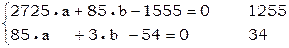
Метод наименьших квадратов в описанном виде применяется только к линейным уравнениям. Одной из задач этого метода является приведение уравнений к линейному виду относительно неизвестных.
Пусть из наблюдений получена совокупность значений xi и yi и известно, что значения связаны функцией 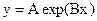 . Найти наилучшие A и B.
. Найти наилучшие A и B.
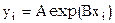
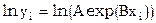
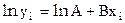
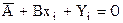 , где
, где 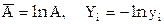
Методом наименьших квадратов решается система
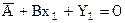
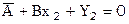
… … … …
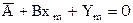 относительно
относительно  . Окончательно
. Окончательно 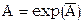 .
.
Пусть из наблюдений получена совокупность значений xi и yi и известно, что значения yi удовлетворяют нормальному закону распределения вероятности Гаусса. Найти коэффициенты в формуле распределения Гаусса
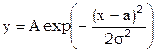 .
.
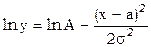
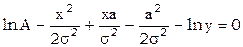
введем обозначения 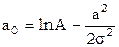
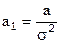
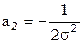
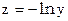
тогда получим систему условных уравнений:
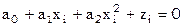 , решая которую методом наименьших квадратов получим
, решая которую методом наименьших квадратов получим 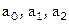 , из которых найдем параметры нормального распределения
, из которых найдем параметры нормального распределения 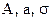 .
.
Пример Из наблюдений получено
| xi | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 | 2.20 | 2.40 | 2.60 | 2.80 | 3.00 |
| yi | 0.120 | 0.412 | 0.977 | 1.812 | 2.637 | 3.008 | 2.635 | 1.816 | 0.985 | 0.417 | 0.121 |
Вычисляем 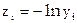 ,
, 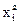
| xi | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
| xi2 | 1.00 | 1.44 | 1.96 | 2.56 | 3.24 | 4.00 |
| zi | 2.1203 | 0.8867 | 0.0233 | -0.5944 | -0.9696 | -1.1013 |
| xi | 2.20 | 2.40 | 2.60 | 2.80 | 3.00 | |
| xi2 | 4.84 | 5.76 | 6.76 | 7.84 | 9.00 | |
| zi | -0.9689 | -0.5966 | 0.0151 | 0.8747 | 2.1120 |
Составляем условные уравнения (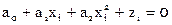 ):
):
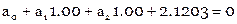
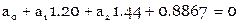
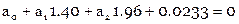
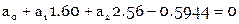
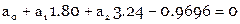
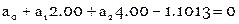
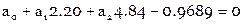
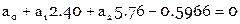
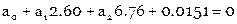
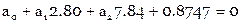
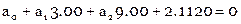
Нормальные уравнения
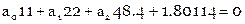
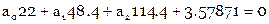
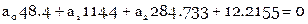
Их решение: 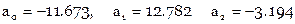
отсюда 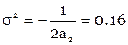 ,
, 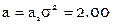 ,
, 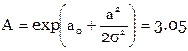 .
.
Итак 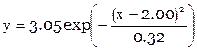 .
.
Если случайные ошибки измерений 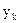 удовлетворяют нормальному закону распределения, то применение принципа Лежандра дает наиболее вероятные значения неизвестных.
удовлетворяют нормальному закону распределения, то применение принципа Лежандра дает наиболее вероятные значения неизвестных.
|
|
|
Если вычислена сумма квадратов невязок 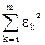 , то средняя погрешность одного условного уравнения s:
, то средняя погрешность одного условного уравнения s:
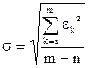 , (m – число уравнений, n – число неизвестных) [6]
, (m – число уравнений, n – число неизвестных) [6]
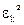 вычисляют еще и для того, чтобы найти грубо ошибочные условные уравнения (если они есть). Если какое-либо
вычисляют еще и для того, чтобы найти грубо ошибочные условные уравнения (если они есть). Если какое-либо 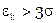 , то вероятно в соответствующем условном уравнении есть грубая ошибка, такие уравнения отбрасывают. После это заново составляют нормальные уравнения и повторяют решение.
, то вероятно в соответствующем условном уравнении есть грубая ошибка, такие уравнения отбрасывают. После это заново составляют нормальные уравнения и повторяют решение.
содержание
 2015-05-14
2015-05-14 812
812








