2015-05-14
2266
Предположим, имеется таблица из двух столбцов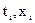 
, 
, 
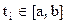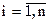. Требуется найти полином низшей степени, который принимает значения 
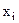для каждого аргумента 
: 
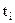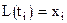, то есть совпадающий со значениями табличной функции в узлах. Приближенно будем считать, что для любого значения аргумента t 
, 
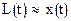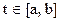. Подобное приближенное равенство называют интерполяционной формулой. Итак, надо найти интерполяционную формулу, а затем оценить ее погрешность.
Найдем, прежде всего, полином (многочлен), который принимает значение 1 в одной узловой точке и 0 во всех других. Очевидно несложная функция
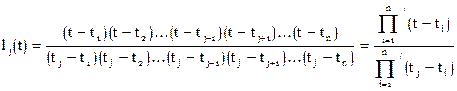, [7]
где штрих у знака произведения означает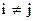 
, является требуемым полиномом степени n-1.
Заметим, что через n точек однозначно можно провести полином степени не выше n-1, например, через 2 точки можно однозначно провести прямую (кривую 1-го порядка), через 3 точки – параболу (кривую 2-го порядка) и т.д.
Легко проверить, что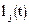 
равен 1, если 
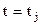; и 0, когда 
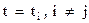. Домножим 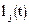на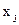 
, полученный полином 
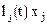принимает значение 
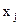в j-й узловой точке и равен нулю во всех других узлах. Поэтому сумма таких полиномов будет принимать значения 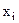для аргумента :
,
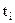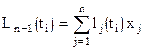Отметим: j – порядковый номер промежуточного полинома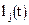 
в сумме, строящей полином Лагранжа; i – номер любого узла таблицы.
В общем случае
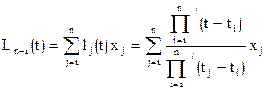[8]
Это и есть искомый полином степени n-1, проходящий через все n узлов таблицы :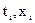 
, .
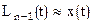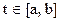Впервые интерполяционный полином Лагранжа был опубликован в 1795 году.
Подчеркнем: если дано n узловых точек, то соответствующий полином степени n-1, проходящий через эти точки, однозначно (в пределах ошибок округления) определен, независимо от способа построения и системы обозначений. Если используются разные узловые точки, то, конечно, полиномы могут быть различными, но одинаковые узловые точки должны приводить к одинаковым полиномам (в пределах ошибок округления).
Потребовав, чтобы полином принимал значения 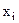для каждого аргумента 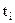, мы построили полином Лагранжа. Если потребовать, чтобы полином принимал не только значения табличной функции в узлах, но и первая производная от полинома была равна первой производной табличной функции в узлах, то мы построим полином Эрмита.
Пример. Дана таблица
| t | x |
Построить интерполяционный полином Лагранжа и найти значение L (2).
n=2. Согласно [8]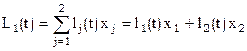 
;
Согласно [7]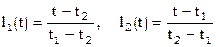 
; 
.
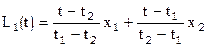Или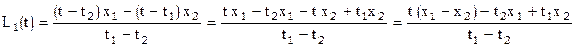 
,
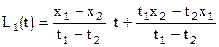. Подставляя числа
.
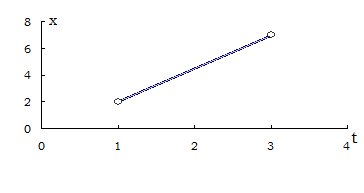
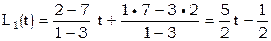Это интерполяционный полином 1-го порядка – прямая.
Для t = 2, L = 4.5.
Пример. Дана таблица
| t | x |
Построить интерполяционный полином Лагранжа и найти значение L (2).
n=3. Согласно [8]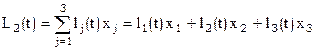 
;
Согласно [7]
;
,
.
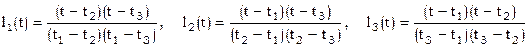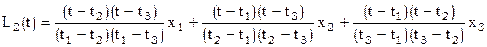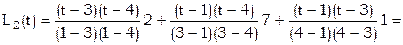
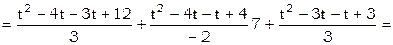
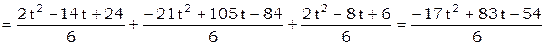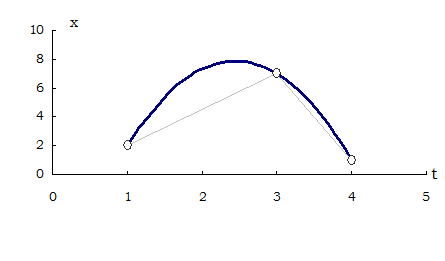
Это интерполяционный полином 2-го порядка – парабола.
Для t = 2, L = 7.33.
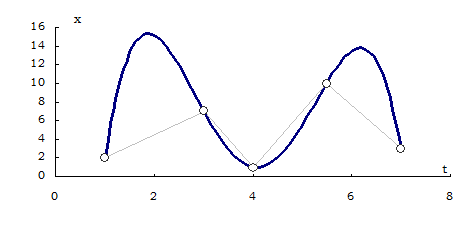
На этом рисунке показан график полинома Лагранжа, построенного по 5-ти узлам – полином 4-го порядка.
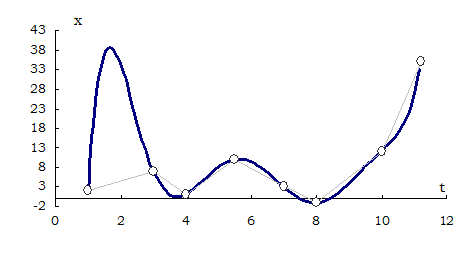
На этом рисунке показан график полинома Лагранжа, построенного по 8-ти узлам – полином 7-го порядка.
Из рисунков видно, что значения табличной функции между узлами полиномом Лагранжа представляются неудовлетворительно. Кроме того, полином Лагранжа неудобен для практического использования. На практике обычно известна требуемая точность результата, а множество используемых узлов можно выбирать.
