Название метода происходит от латинского слова iteratio, что означает «повторение» (iter - шаг). Заменим уравнение [22] 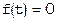 эквивалентным ему уравнением
эквивалентным ему уравнением 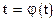 (канонический вид).
(канонический вид).
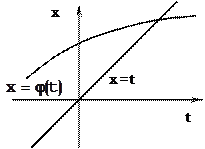 Построим графики обеих частей уравнения
Построим графики обеих частей уравнения 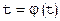 . Для левой части это, очевидно, прямая x = t, являющаяся биссектрисой первого координатного угла. Для правой части график есть некоторая линия с уравнением
. Для левой части это, очевидно, прямая x = t, являющаяся биссектрисой первого координатного угла. Для правой части график есть некоторая линия с уравнением 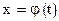 . Решением уравнения является абсцисса точки пересечения этих графиков. Точек пересечения может быть не одна, а несколько.
. Решением уравнения является абсцисса точки пересечения этих графиков. Точек пересечения может быть не одна, а несколько.
Допустим, что каким-либо способом найдено начальное приближение t0. В простейшем методе итераций все дальнейшие приближения строятся по формуле
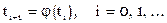 [23]
[23]
Этот процесс называется простой одношаговой итерацией.
Предположим, что значение 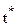 является точным решением уравнения [22], тогда погрешности
является точным решением уравнения [22], тогда погрешности 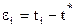 должны быть малыми и по мере итераций уменьшаться. Найдем зависимость между
должны быть малыми и по мере итераций уменьшаться. Найдем зависимость между 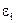 и
и 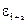 . Очевидно
. Очевидно
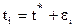 ,
,
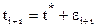 , подставим это в [23], получим
, подставим это в [23], получим
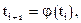
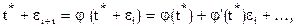
учитывая 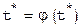 и пренебрегая высшими производными,
и пренебрегая высшими производными,
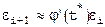 .
.
Итак, если 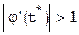 , то
, то 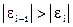 и приближение
и приближение 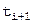 будет отстоять от точного решения
будет отстоять от точного решения 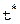 дальше, чем
дальше, чем 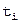 . В этом случае нет сходимости последовательности
. В этом случае нет сходимости последовательности 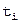 к
к 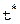 .
.
если 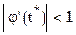 , то
, то 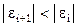 и можно ожидать, что последовательность
и можно ожидать, что последовательность 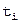 , если
, если 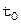 выбрано достаточно близким к
выбрано достаточно близким к 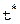 , будет сходиться к
, будет сходиться к 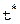 . Причем, при
. Причем, при 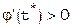
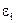 и
и 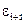 будут иметь одинаковые знаки и сходимость
будут иметь одинаковые знаки и сходимость 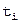 к
к 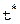 будет монотонной; при
будет монотонной; при 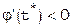
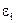 и
и 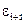 будут иметь разные знаки и
будут иметь разные знаки и 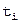 сходится к
сходится к 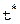 , колеблясь около
, колеблясь около 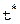 .
.
случай 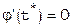 требует специального рассмотрения.
требует специального рассмотрения.
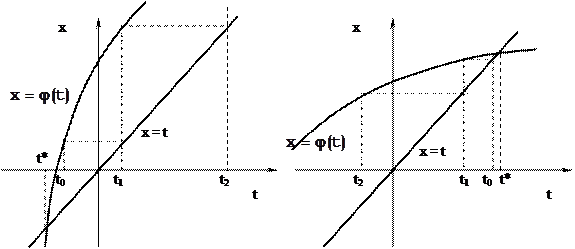
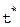 - точное решение;
- точное решение;
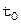 - приближенное решение.
- приближенное решение.
Пример. В небесной механике часто приходится решать уравнение Кеплера вида
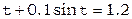 , где t – угол.
, где t – угол.
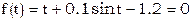 ,
,
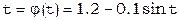 ,
,
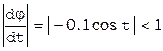 - итерационный процесс сходится,
- итерационный процесс сходится,
в качестве приближенного решения возьмем 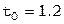 ,
,
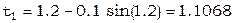
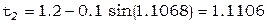
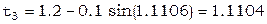
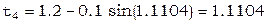
Итак, решение 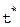 =1.1104.
=1.1104.
Система 2-х уравнений с двумя неизвестными

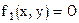
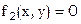
предположим, что эту систему можно представить в виде

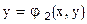
процесс итераций сходится только в случае, если
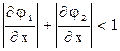

Приближенное решение 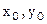 можно найти графически как координаты точки пересечения графиков функций
можно найти графически как координаты точки пересечения графиков функций 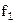 и
и 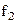 . Тогда
. Тогда
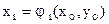
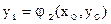
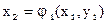
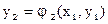 и т.д.
и т.д.
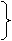 Пример. Дана система уравнений
Пример. Дана система уравнений 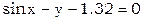
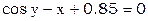
Найти решение.
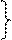
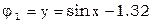
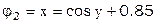
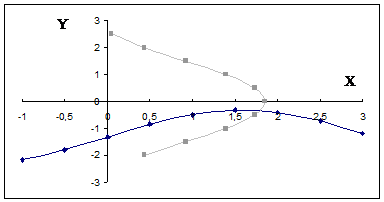
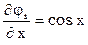 ;
; 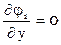 ;
;
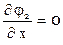 ;
; 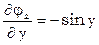 .
.
Проверим
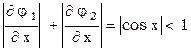 и
и
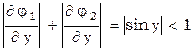 , решение должно сходиться, за исключением точек, где
, решение должно сходиться, за исключением точек, где 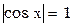 и
и 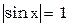 , это сомнительные точки.
, это сомнительные точки.
В качестве нулевого приближения выберем решение
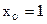
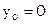
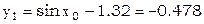
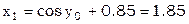
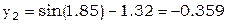
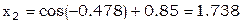
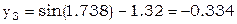
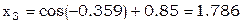
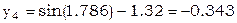
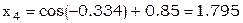
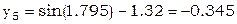
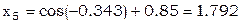
 2015-05-14
2015-05-14 546
546








