Функция 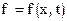 задана таблицей своих значений; значения
задана таблицей своих значений; значения 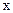 заданы с шагом
заданы с шагом 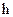 , значения
, значения 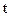 - с шагом
- с шагом 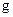 . Табличные значения функции –
. Табличные значения функции – 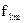 , индекс
, индекс 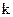 – для
– для 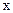 , индекс
, индекс 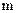 – для
– для 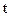 ,
, 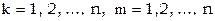 . Требуется найти значение функции для некоторых
. Требуется найти значение функции для некоторых 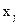 и
и 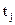 , несовпадающих с узлами таблицы.
, несовпадающих с узлами таблицы.
Эту задачу можно решить, интерполируя 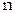 раз по
раз по 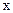 при нескольких табличных значениях
при нескольких табличных значениях 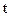 одним из методов точечного интерполирования. Так получим таблицу
одним из методов точечного интерполирования. Так получим таблицу 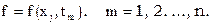
| t1 | f=f(xj,t1) |
| t2 | f=f(xj,t2) |
| … | … |
| tn | f=f(xj,tn) |
Теперь осталось найти значение 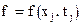 как было сделано выше.
как было сделано выше.
Пример. Задана функция двух переменных
 x t x t | 0.340 | 0.360 | 0.380 | 0.400 | 0.420 | 0.440 |
| 43.380 | 44.443 | 45.540 | 46.671 | 47.838 | 49.037 | |
| 49.901 | 51.038 | 52.205 | 53.399 | 54.620 | 55.867 | |
| 56.185 | 57.371 | 58.580 | 59.810 | 61.059 | 62.326 | |
| 62.238 | 63.451 | 64.681 | 65.925 | 67.181 | 68.447 | |
| 68.071 | 69.294 | 70.527 | 71.768 | 73.015 | 74.265 | |
| 73.697 | 74.916 | 76.138 | 77.363 | 78.588 | 79.813 |
Найти значение функции 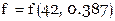
Проинтерполируем 6 раз по столбцам и найдем 6 значений функции для 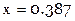 :
:
 x t x t | 0.340 | 0.360 | 0.380 | 0.387 | 0.400 | 0.420 | 0.440 |
| 43.380 | 44.443 | 45.540 | 45.932 | 46.671 | 47.838 | 49.037 | |
| 49.901 | 51.038 | 52.205 | 52.620 | 53.399 | 54.620 | 55.867 | |
| 56.185 | 57.371 | 58.580 | 59.008 | 59.810 | 61.059 | 62.326 | |
| 62.238 | 63.451 | 64.681 | 65.115 | 65.925 | 67.181 | 68.447 | |
| 68.071 | 69.294 | 70.527 | 70.961 | 71.768 | 73.015 | 74.265 | |
| 73.697 | 74.916 | 76.138 | 76.566 | 77.363 | 78.588 | 79.813 |
Так получим таблицу 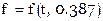
|
|
|
 x t x t | 0.387 |
| 45.932 | |
| 52.620 | |
| 59.008 | |
| 65.115 | |
| 70.961 | |
| 76.566 |
По этой таблице несложно найти значение функции для 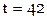 :
:
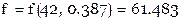 .
.
Можно проконтролировать вычисления, изменив порядок интерполирования – вначале найти таблицу 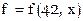 , а затем
, а затем 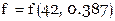 . Результат должен быть тем же.
. Результат должен быть тем же.
ДИФФЕРЕНЦИРОВАНИЕ ПО ТАБЛИЦЕ
Интерполяционными формулами как приближением табличной функции можно воспользоваться для приближенного вычисления производной приближаемой функции в произвольной точке. Интерполяционный полином строится обычно для нормированного значения аргумента 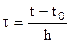 . Обозначим интерполяционный полином через
. Обозначим интерполяционный полином через 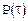 , а интерполируемую функцию
, а интерполируемую функцию 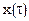 . Тогда
. Тогда
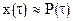 ,
, 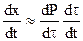 ,
, 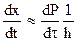 ,
, 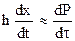 .
.
Аналогично 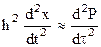 .
.
Найдем производные с использованием формулы Стирлинга. Выпишем ее в виде, предшествующем [14]
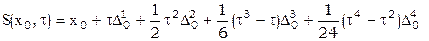 .
.
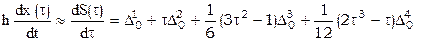 .
.
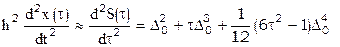 . [18]
. [18]
В простейшем случае, ограничиваясь первыми слагаемыми, имеем
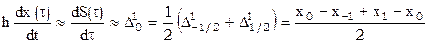 ,
,
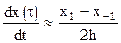 ; [19a]
; [19a]
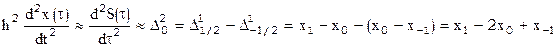 ,
,
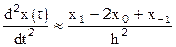 . [19b]
. [19b]
Если требуется вычисление производных вблизи начала таблицы, то придется использовать формулу Ньютона для интерполирования «вперед» [16]:
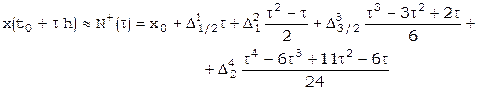
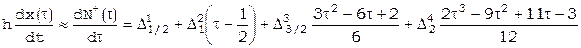 ,
,
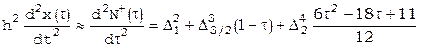 . [20]
. [20]
Если требуется вычисление производных вблизи конца таблицы, то придется использовать формулу Ньютона для интерполирования «назад» [17]:
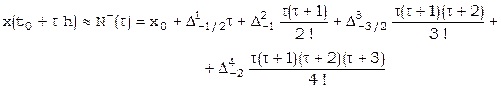 ,
,
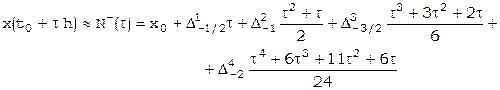
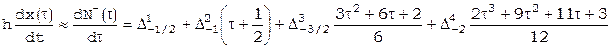
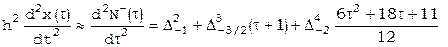 . [21]
. [21]
Пример. Пусть требуется вычислить значение 1-й 2-й производной x при t=0.05 по формуле Стирлинга.
h=0.1, примем t0=0, поэтому 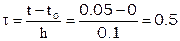 . Из [12]
. Из [12]
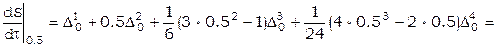
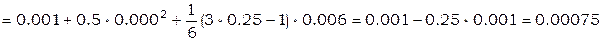
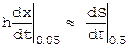 ,
, 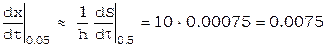 .
.
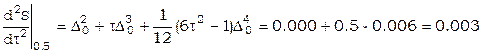 ,
,
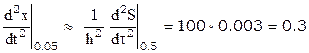 .
.
Таким образом, можно находить производные m-го порядка. Очевидно, что порядок искомой производной должен быть не больше порядка используемых разностей. Если порядок производной больше табличных разностей, то она тождественно обращается в 0.
|
|
|
содержание
 2015-05-14
2015-05-14 737
737








