2015-05-14
442
Метод Ньютона применим к решению очень широкого класса нелинейных уравнений. Значение его в том, что он позволяет привести решение нелинейного уравнения к решению последовательности линейных уравнений.
Рассмотрим уравнение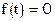 
. Пусть 
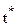- точное решение; 
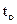- приближенное решение. Очевидно погрешность решения 
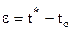, и как правило это малая величина.
,
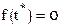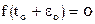, разложим левую часть по степеням 
.
,
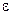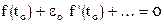решая это уравнение относительно 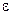, найдем приближенное значение погрешности 
и сможем улучшить значение 
: 
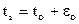, относительно которого можно ожидать, что оно будет ближе к 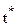, чем :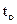
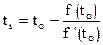
Аналогично можно улучшить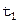 
и т.д.
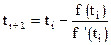[24]
Чтобы последовательные приближения сходились, необходимо чтобы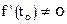 
.
Геометрический смысл правила [24] весьма прост. Построим график функции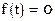 
. Точное решение 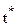это абсцисса точки пересечения графика с осью ОТ. Рассмотрим на этом графике произвольную точку 
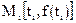и проведем в ней касательную 
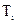. Уравнение касательной есть
.
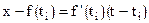Касательная пересечет ось ОТ в точке (ti+1,0), или из уравнения касательной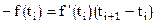 
. Откуда найдем 
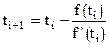, что совпадает с [23]. Таким образом, правило Ньютона геометрически означает, что следующее приближение 
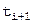находится, если функцию заменить прямой 
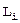, касающейся графика в точке 
.
Пример. Решить уравнение Кеплера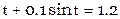 
методом Ньютона.
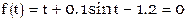
выберем t0=1.2, тогда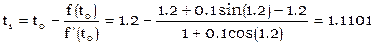 
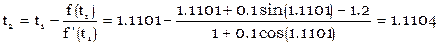
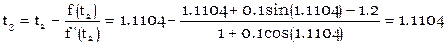
ПОИСК МИНИМУМА ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Функция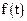 
имеет локальный минимум 
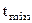на множестве 
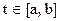, если для всех значений 
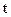верно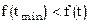 
.
Функция 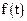должна быть непрерывной или кусочно-непрерывной, иначе сложно построить метод поиска ее минимума. Если 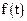не является кусочно-непрерывной, то единственным способом решения задачи является перебор всех элементов 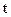, на которых задана функция. Вообще, чем более жестким требованиям удовлетворяет 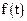, тем легче строить хорошие численные алгоритмы.
