2015-05-14
568
Изменение внутренней энергии газа
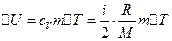, (1)
где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i =5);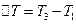 
- разность температур газа в конечном (третьем) и начальном состояниях.
Начальную и конечную температуру газа найдём из уравнения Менделеева – Клапейрона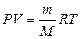 
, откуда
, 
, 
.
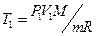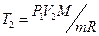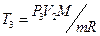Работа расширения газа при постоянном давлении выражается формулой
.
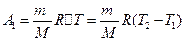Работа газа, нагреваемого при постоянном объеме равна нулю:
A2 = 0.
Следовательно полная работа, совершаемая газом равна
А = А1 + А2 = А1.
Согласно первому началу термодинамики, теплота Q передаваемая газу, равна сумме изменения внутренней энергии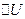 
и работы А:
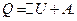
Произведём вычисления, учтя, что для кислорода
M =32·10-3 кг/моль, получим
; 
; 
.
;
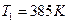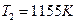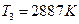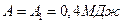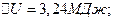
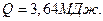
График процесса представлен на рисунке.
Пример 4. В цилиндре под поршнем находится водород массой m = 0,02 кг при температуре Т1 = 300 К. Водород сначала расширялся адиабатно, увеличив свой объём в n1 =5 раз, а затем был сжат изотермически, причём объём газа уменьшился в n2 =5 раз. Найти температуру в конце адиабати- ческого расширения и работу, совершаемую газом при этих процессах. Изобразить процесс графически.
