1. Определите выражение функции, используя знак присвоения и указав явную зависимость функции от аргумента.
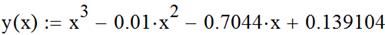
2. Затем постройте график функции, используя панель инструментов графики

На панели используйте кнопку Декартов график  , затем заполните в области графика поля под осью ОХ именем переменной и рядом с осью ОУ- именем функции. Отформатируйте область графика, установив стиль осей – по центру. Под осью ОХ измените диапазон изменения переменной х – от -1 до 1.
, затем заполните в области графика поля под осью ОХ именем переменной и рядом с осью ОУ- именем функции. Отформатируйте область графика, установив стиль осей – по центру. Под осью ОХ измените диапазон изменения переменной х – от -1 до 1.
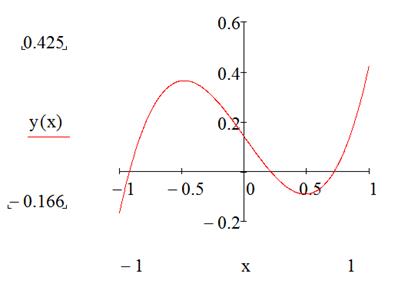
3. После визуального исследования области графика выясняется, что на отрезке [-1;1] функция имеет три корня, поскольку трижды пересекает ось ОХ. Для точного вычисления корней уравнения необходимо из графика определить примерные значения корней, а затем использовать их в качестве начальных приближений для уточнения их значений.
Первое приближение можно взять равным -0,9, второе будет равно 0,3, третье можно взять равным 0,7.
4. Для уточнения приближенных значений используем функцию root
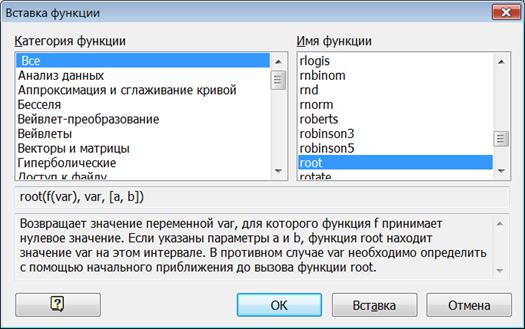
Задаем первое приближение переменной 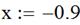 , а затем с помощью функции root получаем его точное значение
, а затем с помощью функции root получаем его точное значение 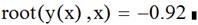
5. Задаем второе приближение 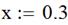 , а затем аналогично получаем точное значение второго корня
, а затем аналогично получаем точное значение второго корня 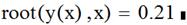
6. Задаем третье приближение 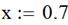 , получаем точное значение третьего корня
, получаем точное значение третьего корня 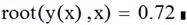
 2015-05-14
2015-05-14 653
653








