Основой для микроскопического (микромагнитного) описания движения магнитных моментов в ДГ является уравнение Ландау-Лифшица:
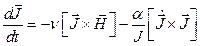
Где n - гиромагнитное отношение. Первый член – вектор, перпендикулярный векторам J и H (рис. 2)., второе слагаемое описывает движение в направлении тормозящей силы. Коэффициент a задает величину затухания и измеряется в герцах.
Если нет затухания уравнение перепишется:
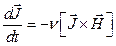
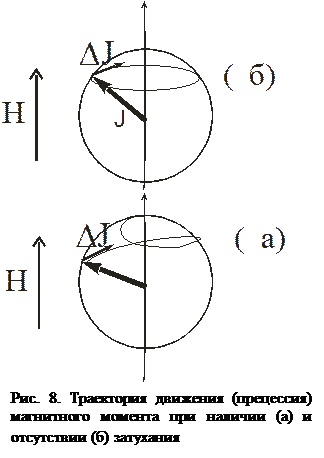 Оно описывает прецессию намагниченности вокруг поля H (рис. 27 б). Если затухание присутствует, то J будет прецессировать вокруг H, постепенно приближаясь к нему (рис. 8 а).
Оно описывает прецессию намагниченности вокруг поля H (рис. 27 б). Если затухание присутствует, то J будет прецессировать вокруг H, постепенно приближаясь к нему (рис. 8 а).
Рассмотрим доменную границу в одноосном кристалле (рис. 6). Приложим магнитное поле, параллельно ОЛН. Согласно уравнению Ландау-Лифшица вектор m начинает прецессию вокруг поля H (рис. 1), создавая при этом поле рассеяния, H m перпендикулярное, поверхности ДГ.
Исходя из модели Блоха: 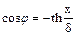 и небольшого постоянного значения H m (угол y - постоянный), что означает стационарное движение доменной границы Ландау и Лифшиц получили:
и небольшого постоянного значения H m (угол y - постоянный), что означает стационарное движение доменной границы Ландау и Лифшиц получили: 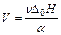 или
или 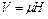 , где подвижность
, где подвижность 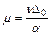
При приложении импульса магнитного поля в форме ступеньки угол y постепенно достигает максимального значения, а после окончания действия поля, вектор m не сразу возвращается в равновесное состояние (в плоскости стенки).
Такую инерционность стенки в уравнениях движения с ускорением можно связать с массой Деринга: 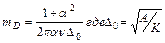 .
.
Скорость при стационарном движении пропорциональна углу y. Этот угол может меняться в ограниченных пределах, поэтому предельная скорость ДГ имеет ограничение. Предельная скорость Уокера 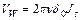 такая скорость достигается в магнитном поле величиной
такая скорость достигается в магнитном поле величиной 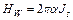
 2015-05-14
2015-05-14 1032
1032








