 |
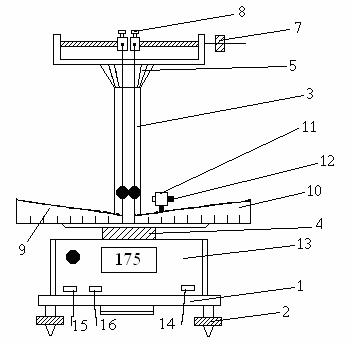
Основание 1 оснащено регулируемыми ножками 2, которые позволяют провести выравнивание прибора. В основании закреплена колонка 3, на
Рис. 1
которой зафиксированы нижнийкронштейн 4 и верхний кронштейн 5. На верхнем кронштейне закреплены стержни, на которых подвешены шары. Винт 7 позволяет менять расстояние между шарами. С помощью винта 8 можно изменять длину подвески шаров. На нижнем кронштейне закреплены угольники со шкалами 9, 10 и электромагнит 11. Электромагнит можно передвигать вдоль правой шкалы и менять высоту его установки. Силу притяжения электромагнита можно регулировать винтом 12. Угольники со шкалами также можно передвигать вдоль нижнего кронштейна.
К основанию прибора привинчен цифровой микросекундомер 13, измеряющий время соударения (взаимодействия) шаров. На лицевой панели прибора расположены три клавиши: 14 (сеть) – выключатель сети; 15 (пуск) – отключение электромагнита и запуск секундомера; 16 (сброс) – включение электромагнита и подготовка микросекундомера к следующему измерению.
ЗАДАНИЕ № 1
Цель работы: проверить закон сохранения импульса.
В изолированной системе тел векторная сумма импульсов всех тел, входящих в систему (импульс системы), не изменяется с течением времени:
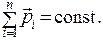
Если на тела системы действуют внешние силы, то импульс равнодействующей внешних сил 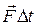 равен изменению импульса системы:
равен изменению импульса системы:
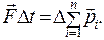
В данной работе шары, подвешенные на нитях, нельзя рассматривать как изолированную систему, но для небольшого промежутка времени, порядка времени удара, импульсом внешних сил можно пренебречь. Поэтому систему тел можно считать практически изолированной, для которой выполняется закон сохранения импульса:
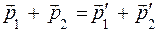 ,
,
где
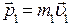 – импульс первого шара перед ударом;
– импульс первого шара перед ударом;
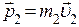 – импульс второго шара перед ударом;
– импульс второго шара перед ударом;
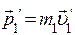 – импульс первого шара после удара;
– импульс первого шара после удара;
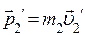 – импульс второго шара после удара.
– импульс второго шара после удара.
В проекциях на ось OX это соотношение имеет вид
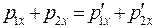 .
.
Определим импульс системы 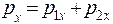 до удара и импульс системы
до удара и импульс системы 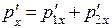 после удара и сравним их. Для этого рассмотрим движение шара массой m 1, подвешенного на нити в поле тяготения Земли, отклонив шар от положения равновесия на угол a1 (рис. 2). Сила натяжения нити работы не совершает, так как все время движения она перпендикулярна к траектории. Следовательно, к движению шара можно применить закон сохранения энергии
после удара и сравним их. Для этого рассмотрим движение шара массой m 1, подвешенного на нити в поле тяготения Земли, отклонив шар от положения равновесия на угол a1 (рис. 2). Сила натяжения нити работы не совершает, так как все время движения она перпендикулярна к траектории. Следовательно, к движению шара можно применить закон сохранения энергии
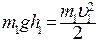 ,
,
где h 1 – высота, на которую был поднят шар; g – ускорение свободного падения; u 1 – скорость первого шара перед самым ударом.
Тогда
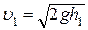 .
.
Из треугольника OAB (см. рис. 2) следует
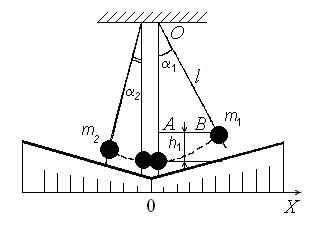
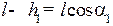 ,
,
где l – расстояние от точки подвеса шара до его центра тяжести.
Определим h 1:
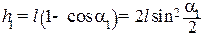 .
.
Следовательно,
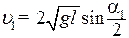 . (1)
. (1)
Рис. 2
Так как второй шар с массой m 2 до удара находился в состоянии покоя, то импульс системы перед ударом равен
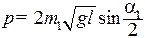 . (2)
. (2)
После упругого столкновения шаров первый шар приобретает скорость 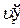 , второй шар – скорость
, второй шар – скорость 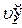 , которые можно узнать по углам их отклонения α1' и a2¢. (Вывод аналогичен выводу u 1):
, которые можно узнать по углам их отклонения α1' и a2¢. (Вывод аналогичен выводу u 1):
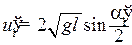 , (3)
, (3)
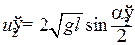 . (4)
. (4)
В проекции на ось OX импульсы шаров после удара будут равны:
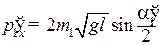 , (5)
, (5)
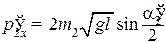 . (6)
. (6)
Если после столкновений первый шар будет двигаться в обратном направлении, тогда угол 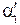 принимает отрицательное значение. Суммарный импульс шаров (импульс замкнутой системы) после упругого удара будет равен
принимает отрицательное значение. Суммарный импульс шаров (импульс замкнутой системы) после упругого удара будет равен
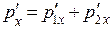 . (7)
. (7)
Сравним импульсы системы до и после удара, найденные по формулам (2) и (7) и убедимся, что 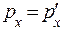 .
. 
ЗАДАНИЕ № 2
Цель работы: определить среднюю силу удара.
Изменение импульса тела равно импульсу средней силы, действующей на тело
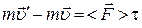 .
.
Применяя эту формулу для ударяемого шара массой m 2, получим (в проекциях на горизонтальную ось)
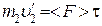 ,
,
где 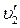 – скорость шара после удара (до столкновения шар находился в покое); < F > – средняя сила удара; t – длительность удара.
– скорость шара после удара (до столкновения шар находился в покое); < F > – средняя сила удара; t – длительность удара.
Определим среднюю силу удара
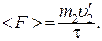
Подставив сюда вместо 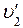 выражение (4), получим расчетную формулу для средней силы удара
выражение (4), получим расчетную формулу для средней силы удара
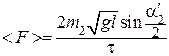 , (8)
, (8)
где l – длина подвеса шара; 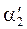 – угол, на который отклоняется второй шар после удара.
– угол, на который отклоняется второй шар после удара.
 2015-05-14
2015-05-14 355
355








