Такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: 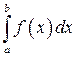 . Но, в отличие от определенного интеграла, подынтегральная функция
. Но, в отличие от определенного интеграла, подынтегральная функция 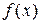 терпит разрыв второго рода:
терпит разрыв второго рода:
1) в точке 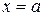 , 2) или в точке
, 2) или в точке 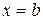 ,
,
3) или в обеих точках сразу, 4) или даже на отрезке интегрирования.
Определение 2. Пусть 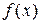 определена на
определена на 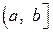 , причем
, причем 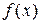 неограниченна в окрестности особой точки
неограниченна в окрестности особой точки 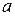 , но она ограничена и интегрируема на любом отрезке
, но она ограничена и интегрируема на любом отрезке 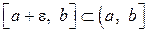 . Тогда если существует предел
. Тогда если существует предел 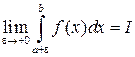 , то он называется несобственным интегралом и обозначается
, то он называется несобственным интегралом и обозначается 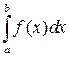 .
.
Если предела нет или он равен бесконечности, то интеграл называется расходящимся.
Аналогично определяется интеграл от функции, неограниченной на верхнем пределе интегрирования: 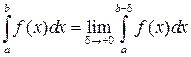 . Наконец, если
. Наконец, если 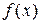 неограниченна в окрестности особой точки
неограниченна в окрестности особой точки 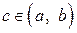 , то
, то
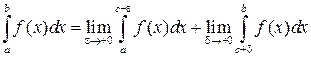 .
.
Пример 3. Исследовать на сходимость интеграл 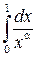 .
.
Решение. 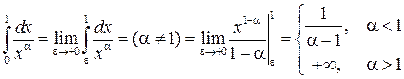 . При
. При 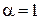 имеем
имеем 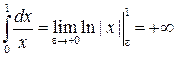 .
.
Таким образом, 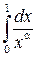 сходится при
сходится при 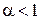 и расходится при
и расходится при 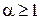 .
.
 2015-05-14
2015-05-14 460
460








