2015-05-14
607
Первая теорема сравнения. Пусть на отрезке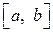 
функци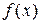и 
и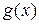 
разрывны в точке 
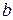, и для каждого 
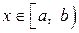выполняется неравенство 
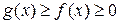. Тогда если сходится 
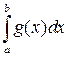, то сходится и 
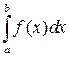; если расходится 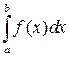, то расходится и .
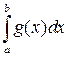Вторая теорема сравнения. Пусть на отрезке 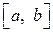функци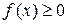и 
и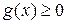 
разрывны в точке 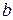, и пусть существует 
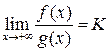. Тогда:
1) Если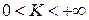 
, то 
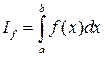и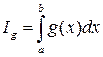 
сходятся или расходятся одновременно.
2) Если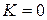 
, то из сходимости 
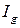следует сходимость 
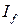, а из расходимости 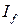следует расходимость .
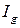3) Если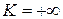 
, то из сходимости 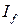следует сходимость 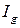, а из расходимости 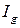следует расходимость .
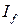Пример 4. Исследовать сходимость интеграла Эйлера—Пуассона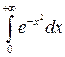 
.
Решение.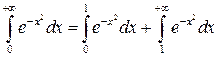 
. Первый интеграл в правой части сходится. При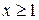 
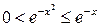. Так как 
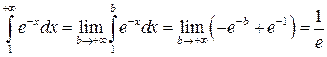, то по первой теореме сравнения интеграл 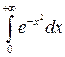сходится.
Пример 5. Исследовать на сходимость интеграл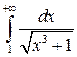 
.
Решение. Если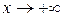 
, то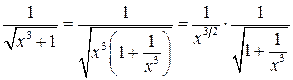 
. В качестве мажорирующей функции возьмем 
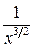. Так как 
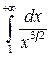сходится, то сходится исходный интеграл.
Пример 6. Исследовать на сходимость интеграл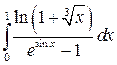 
.
Решение. Подынтегральная функция в промежутке интегрирования положительна и при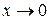 
стремится к бесконечности. Пользуясь теоремой об эквивалентных бесконечно малых, преобразуем числитель и знаменатель подынтегральной дроби. Имеем:
|
|
|
, 
, 
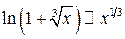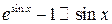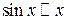при .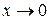
Откуда получаем эквивалентность функций
.
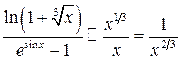По признаку сравнения можно исследовать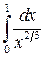 
, который сходится.
Поэтому сходится и исходный интеграл.
