Если сходятся интегралы 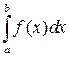 и
и 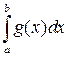 , где
, где 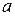 и
и 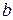 могут принимать значения
могут принимать значения 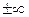 , то
, то
1. 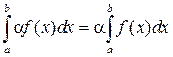 , где
, где 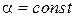 .
.
2. 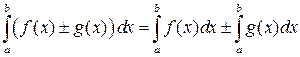 .
.
Несобственные интегралы в левых частях сходятся, и их значения равны выражениям в правых частях.
Рассмотрим 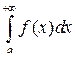 . Пусть
. Пусть 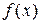 непрерывна на любом отрезке вида
непрерывна на любом отрезке вида 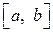 , где
, где 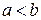 . Тогда интегралы
. Тогда интегралы 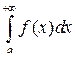 и
и 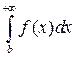 сходятся или расходятся одновременно. Аналогичное утверждение можно сформулировать и для несобственных интегралов от неограниченных функций и конечного отрезка интегрирования.
сходятся или расходятся одновременно. Аналогичное утверждение можно сформулировать и для несобственных интегралов от неограниченных функций и конечного отрезка интегрирования.
Интегралы от знакопостоянных функций.
Все теоремы сформулированы для положительных функций, однако они справедливы для знакопостоянных функций.
Теоремы сравнения.
 2015-05-14
2015-05-14 1563
1563








