Первая теорема сравнения. Пусть 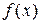 и
и 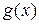 определены на
определены на 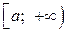 , интегрируемы на любом отрезке
, интегрируемы на любом отрезке 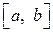 , где
, где 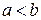 и
и 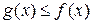 , причем
, причем 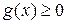 . Тогда:
. Тогда:
1. если сходится 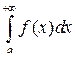 , то сходится и
, то сходится и 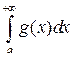 ;
;
2. если расходится 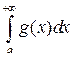 , то расходится и
, то расходится и 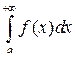 .
.
Вторая теорема сравнения. Пусть функции 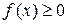 и
и 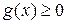 определены на
определены на 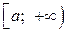 , и пусть существует
, и пусть существует 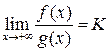 . Тогда
. Тогда
1) Если 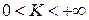 , то
, то 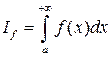 и
и 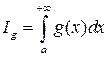 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
2) Если 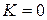 , то из сходимости
, то из сходимости 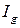 следует сходимость
следует сходимость 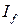 , а из расходимости
, а из расходимости 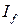 следует расходимость
следует расходимость 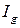 .
.
3) Если 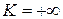 , то из сходимости
, то из сходимости 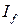 следует сходимость
следует сходимость 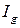 , а из расходимости
, а из расходимости 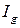 следует расходимость
следует расходимость 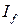 .
.
 2015-05-14
2015-05-14 601
601








