Для характеристики размера ядра используется понятие среднеквад-ратичного электрического радиуса, в котором учитывается распределение плотности ядерного вещества. Если считать, что ядро представляет собой сферу однородной плотности, то ее радиус будетопределяться следующим образом: 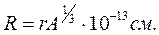 , где r-область действия ядерных сил, выраженных в единицах Ферми.
, где r-область действия ядерных сил, выраженных в единицах Ферми.
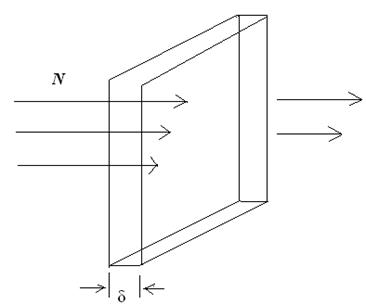 В данном случае исследуется столкновение пучка частиц с мишенью, что дает возможность определения радиуса ядра. Мишень настолько тонкая, что ядра не перекрывают друг друга. В данном процессе появляется новый параметр, характеризующий столкновение падающих частиц падающих частиц с ядрами мишени.
В данном случае исследуется столкновение пучка частиц с мишенью, что дает возможность определения радиуса ядра. Мишень настолько тонкая, что ядра не перекрывают друг друга. В данном процессе появляется новый параметр, характеризующий столкновение падающих частиц падающих частиц с ядрами мишени.
Физический смысл этого параметра: 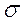 - вероятность взаимодействия, называемое сечением данного процесса. Что же такое
- вероятность взаимодействия, называемое сечением данного процесса. Что же такое 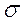 ?
?
Пусть N – поток нейтронов, падающих на см2 мишени, 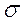 - есть отношение провзаимодействовавших нейтронов к падающему числу нейтронов
- есть отношение провзаимодействовавших нейтронов к падающему числу нейтронов 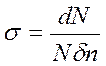 , где dN - число столкновений, δ – толщина пластинки, n – количество ядер в пластинке, следовательно, число провзаимодействовавших частиц равно:
, где dN - число столкновений, δ – толщина пластинки, n – количество ядер в пластинке, следовательно, число провзаимодействовавших частиц равно:
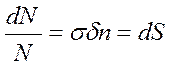 т.е. относительной доле площади мишени. А такая площадь может быть представлена, как геометрическое поперечное сечение:
т.е. относительной доле площади мишени. А такая площадь может быть представлена, как геометрическое поперечное сечение: 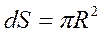
Для такого приравнивания нужно:
1. чтобы длина дебройлевской волны падающей частицы была значительно меньше радиуса ядра 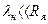 ;
;
2. чтобы каждый нейтрон взаимодействовал с ядром. Следовательно, нейтроны должны обладать небольшой энергией. Эксперимент показывает, что Ен ~20Мэв (<50Мэв). Поэтому из соотношения πR2=σ, зная σ, можно определить радиус ядра. Для свинца 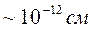 , для железа
, для железа 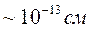 . Если считать, что ядро представляет сферу однородной плотности, то ее радиус R=r0A1/3٠10-13cм. Этим методом получили R=(1,2 – 1,3)A1/3٠10-13cм.
. Если считать, что ядро представляет сферу однородной плотности, то ее радиус R=r0A1/3٠10-13cм. Этим методом получили R=(1,2 – 1,3)A1/3٠10-13cм.
В случае энергии 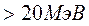 надо вводить поправку на частичное прохождение быстрых нейтронов сквозь ядро. И тогда R=(1,3 – 1,4)A1/3٠10-13cм.
надо вводить поправку на частичное прохождение быстрых нейтронов сквозь ядро. И тогда R=(1,3 – 1,4)A1/3٠10-13cм.
Рассеяние 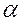 – частиц.
– частиц.
Известно, что ядра с 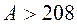 самопроизвольно испускают
самопроизвольно испускают 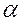 – частицы по следующей схеме:
– частицы по следующей схеме: 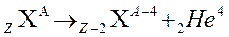 . Для
. Для 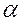 радиоактивных ядер получено полуэмпирическое соотношение, которое связывает время жизни и энергию
радиоактивных ядер получено полуэмпирическое соотношение, которое связывает время жизни и энергию 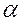 – частицы: lgτ+AlgEα=B. Это соотношение называется соотношением Гейгера – Нэттола. Такая зависимость между Eα и τ объяснялась необходимостью для
– частицы: lgτ+AlgEα=B. Это соотношение называется соотношением Гейгера – Нэттола. Такая зависимость между Eα и τ объяснялась необходимостью для 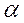 – частицы пройти некоторый потенциальный барьер прежде чем выйти из ядра.
– частицы пройти некоторый потенциальный барьер прежде чем выйти из ядра.
Вероятность прохождения 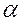 – частицы через барьер с энергией Е пропорциональна коэффициенту прозрачности барьера W, которая имеет вид:
– частицы через барьер с энергией Е пропорциональна коэффициенту прозрачности барьера W, которая имеет вид:
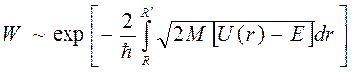
Схему прохождения 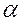 – частицы можно представить в виде
– частицы можно представить в виде
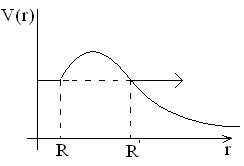
Данная формула позволяет определить радиус ядра. Для точного определения радиуса ядра необходимо ввести поправку на радиус самой 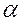 – частицы, т.к. мы предполагаем что
– частицы, т.к. мы предполагаем что 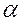 – частица находится внутри ядра. Распределение вещества в процессе
– частица находится внутри ядра. Распределение вещества в процессе 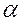 – распада в ядре меняется, поэтому данный метод дает небольшую точность
– распада в ядре меняется, поэтому данный метод дает небольшую точность 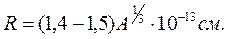
 2015-05-14
2015-05-14 848
848








