Модель парной линейной регрессии: спецификация, условия построения

1 единственная ОП, 1 результирующая переменная

Пусть исходные данные представлены выборкой объема n, содержащей пары наблюдаемых значений (xi, yi), i =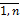

Уравнение парной линейной регрессии для ГС имеет вид yi = 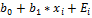, где х - ОП, у- результирующая переменная, Е- ошибка регрессии, в0 и в1- параметры уравнения.

На основе обработки данных выборочного наблюдения получают выборочное уравнение регрессии, которое записывается в виде: yi = 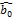+ + 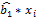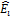, где 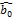, 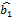- выборочные оценки коэф в1 и в0 функции регрессии ГС.

Модель регрессии или уравнение регрессии позволяет количественно оценить взаимосвязь между исследуемыми переменными.

Задача регрессионного анализа состоит в том, чтобы по данным наблюдений определить такую функцию ỹ = f (x), которая наилучшим образом описывала исследуемую зависимость между переменными.

Модель линейна: по ОП, параметрам и по случайным ошибкам.

При построении нормальной линейной модели парной регрессии учитываются пять условий:

1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии εi;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

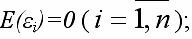
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:

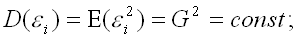
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю): Cov(εi,εj)=E(εi,εj)=0 (). Это условие выполняется в том случае, если исходные данные не являются временными рядами;

5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: εi~N(0, G2).

Общий вид нормальной линейной модели парной регрессии в матричной форме:

Y= X* β+ ε,

где

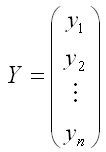
– случайный вектор-столбец значений результативной переменной размерности n x 1;

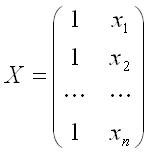
– матрица значений факторной переменной размерности n x 2. Первый столбец является единичным, потому что в модели регрессии коэффициент β0 умножается на единицу;

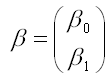
– вектор-столбец неизвестных коэффициентов модели регрессии размерности 2 x 1;

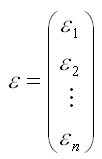
– случайный вектор-столбец ошибок модели регрессии размерности n x 1.

Условия построения нормальной линейной модели парной регрессии, записанные в матричной форме:

1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии βi;

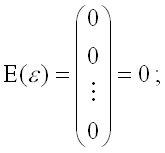
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:;

3) третье и четвёртое условия можно записать через ковариационную матрицы случайных ошибок нормальной линейной модели парной регрессии:

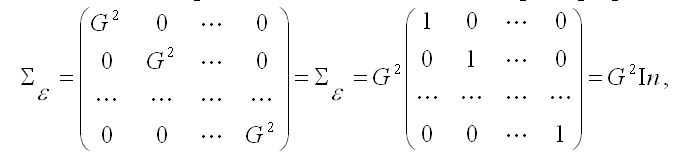
где G2 – дисперсия случайной ошибки модели регрессии ε;

In – единичная матрица размерности n x n.

4) случайная ошибка модели регрессии подчиняется нормальному закону распределения: εi~N(0, G2).