Модели регрессии, нелинейные по оцениваемым коэффициентам

Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели β0…βn.

К моделям регрессии, нелинейными по оцениваемым параметрам, относятся:

1) степенная функция:

2) показательная или экспоненциальная функция:

3) логарифмическая парабола:

4) экспоненциальная функция:

5) обратная функция:

6) и т.д.

Модели регрессии, нелинейные по оцениваемым коэффициентам, делятся на два класса:

1) модели регрессии, которые можно с помощью преобразований привести к линейному виду;

2) модели регрессии, которые невозможно привести к линейному виду.

Для оценки неизвестных параметров моделей регрессии, которые нельзя привести к линейному виду, нельзя применять классический метод наименьших квадратов. В этом случае используются итеративные процедуры оценивания (квази-ньютоновский метод, симплекс-метод, метод Хука-Дживса, метод Розенброка и др.).

Задача множественного корреляционно – регрессионного анализа. Спецификация эконометрической модели множественной регрессии. Условия Гаусса – Маркова для модели множественной регрессии.

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной У от нескольких объясняющих переменных Х1, Х2,…..Хn. Эта задача решается с помощью множественного регрессионного анализа.

У=F(Х1, X2, ….. Xk)+E

Обозначим i-e наблюдение зависимой переменной уi, а объясняющих переменных – xi1, xi2, … xik. Тогда модель множественной линейной регрессии можно представить в виде:

Y=b0+b1X1+b2X2+……+bkXk+E

Предпосылки для множественного регрессионного анализа могут быть записаны следующим образом:

· В матричной форме модели Y=Xb+E, E-случайный вектор, Х- неслучайная (детерминированная) матрица

· M(E)=0

·

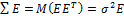
· E-нормально распределенный случайный вектор, то есть Е 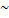N(0;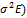

· r(X)=p+1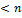

Модель, удовлетворяющая приведенным предпосылкам, называется классической нормальной линейной моделью множественной регрессии.

Теорема Гаусса – Маркова, рассмотренная для парной регрессионной модели, оказывается верной и в общем виде для модели множественной регрессии: при выполнении предпосылок (кроме предпосылки о нормальном распределении) множественного регрессионного анализа оценка МНК b=(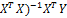 является наиболее эффективной, то есть обладает наименьшей дисперсией в классе линейных несмещенных оценок.