2015-05-18
2634
Для множественной линейной регрессии с числом факторов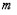 
вычисляют коэффициент детерминации с учетом величины дисперсии на одну степень свободы. В этом случае скорректированный коэффициент детерминации находят по формуле …
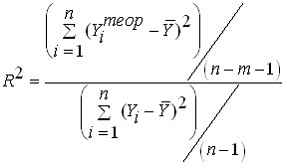
Пусть исследуется линейная зависимость вида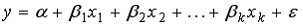 
и оценена регрессия 
, 
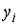– фактические значения, а 
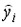– расчетные значения зависимой переменной, 
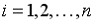. Тогда общую дисперсию можно оценить по формуле …
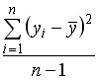
Значение коэффициента детерминации составило 0,9, следовательно …
уравнением регрессии объяснено 90% дисперсии результативного признака y
Значение коэффициента детерминации составило 0,81, следовательно уравнением регрессии объяснено _____ дисперсии зависимой переменной.
81 %
Рассматривается регрессионная модель 
, где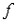 
- линейная функция. Количество наблюдений 
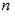=25. Остаточная сумма квадратов равна 440. Тогда остаточная дисперсия на одну степень свободы равна …
Случайными воздействиями обусловлено 12% дисперсии результативного признака, следовательно, значение коэффициента детерминации составило …
|
|
|
0,88
Коэффициент детерминации …
