Тест Дарбина-Уотсона отсутствия автокорреляции случайного остатка в линейной модели множественной регрессии

После оценивания коэффициентов регрессии появляется возможность оценить «остатки» - оценки значений случайной составляющей ε_t, которые мы будем обозначать e_t. Таким образом

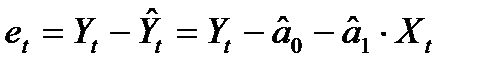
Применяя к остаткам тест Дарбина-Уотсона, мы получаем возможность проверить третью предпосылку теоремы Гаусса-Маркова о некоррелированности случайных величин ε_t при разных t. Для этого вычисляется статистика Дарбина-Уотсона:

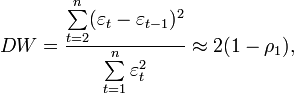
где 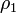— коэффициент автокорреляции первого порядка.

Статистика DW служит инструментом для проверки гипотезы об отсутствии корреляции между соседними значениями последовательности случайных величин e_t. Для проверки гипотезы число DW размещается на одноименной оси в соответствии со своим значением. Границами-ориентирами служат значения d_l и d_u , определяемые по таблице в зависимости от числа наблюдений n в исходных данных и числа k – количества независимых переменных.

В случае отсутствия автокорреляции 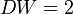, при положительной автокорреляции 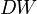стремится к нулю, а при отрицательной — к 4:

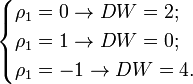
На практике применение критерия Дарбина — Уотсона основано на сравнении величины 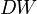с теоретическими значениям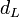и и 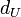для заданных числа наблюдений 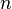, числа независимых переменных модели 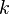и уровня значимости .

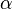1. Если 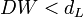, то гипотеза о независимости случайных отклонений отвергается (следовательно присутствует положительная автокорреляция);
2. Если 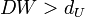, то гипотеза не отвергается;
3. Если 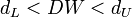, то нет достаточных оснований для принятия решений.

Когда расчетное значение 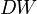превышает 2, то с 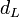и 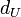сравнивается не сам коэффициент 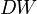, а выражение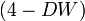

24. Показатели качества регрессии:коэффициент детерминации как мерило качества спецификации эконометрической модели.

Смысл коэффициента детерминации обсудим, не теряя общности, на примере линейной модели парной регрессии (8.1'). Пусть имеется оцененная МНК линейная модель парной регрессии. Пусть имеется оцененная МНК линейная модель парной регрессии,

у= ά₀ + ά1 Х+ U.

(S ά₀) (S ά1) (бu)

Предполагается, что МНК-оценки ее параметров получены по обу­чающей выборке в ситуации, когда все предпосылки теоремы Гаусса — Маркова адекватны.

В уравнении обозначим символом

y = a_Q + aix (12.2)

оценку функции регрессии в модели. Подчеркнем, что регрессор х полностью объясняет левую часть равенства — случайную переменную у. Следовательно, с учетом (12.2) и урав­нений наблюдений (8.4) справедливы равенства:

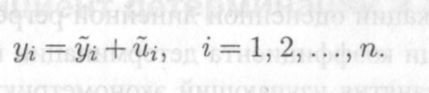12.3

Здесь п — количество уравнений наблюдений (8.4), по которым и найдена МНК-оценка (12.1). Далее первое слагаемое в формуле (12.3) полностью объясняется в рамках данной модели регрессором х; напротив, второе слагаемое никак не объясняется этим регрессо­ром. Поэтому ясно, что объясняющая способность х тем выше", чем большую долю в переменной у составляет первое слагаемое. Как измерить эту долю? Ведь у — переменная величина! Осуществить такую процедуру можно, если привлечь понятие дисперсии.

Согласно свойству (6.61) операции оценивания дисперсии по выборочным данным справедливо равенство

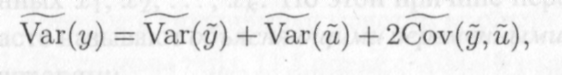(12.4) где

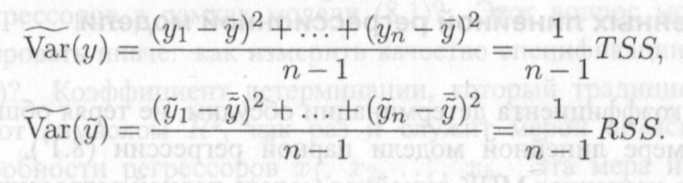12.5

Можно показать (см. задачу 12.2), что, во-первых, последнее слагаемое в правой части равенства (12.4) равно нулю, т.е.

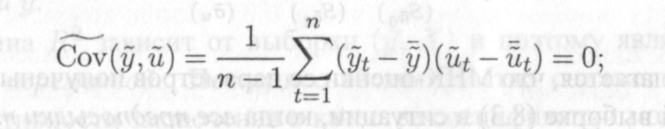12.7

а во-вторых, второе слагаемое в правой части (12.4)

12.8

Следовательно, в качестве меры, объясняющей способности регрессора в модели (8.1'), может служить в пределах обучающей выборки (у, X) величина

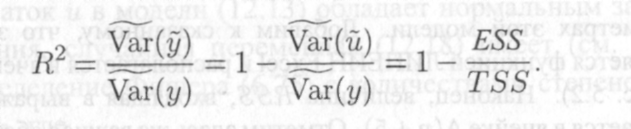12.9

Она именуется коэффициентом детерминации модели и равна доле эмпирической дисперсии переменной у, которая в рамках обучаю­щей выборки (у, X) объясняется в модели (8.1') ее регрессором х. Из равенств (12.5), (12.7) и (12.9) следует, что всегда

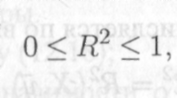12.10

причем если Я2 = 1, то значения уг переменной у полностью объ­ясняются в выборке (у, X) значениями хг регрессора х, поскольку ESS = 0 и, следовательно,

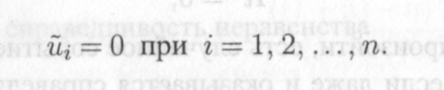12.11

Напротив, когда В? = 0, то спецификация (8.1'), очевидно, совер­шенно плоха, так как в рамках такой модели регрессор х абсолютно неспособен объяснять значения переменной у. Заметим, что ситу­ация совершенно плохой спецификации равносильна справедливо­сти статистической гипотезы (см. занятие 7)

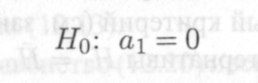12.12

о коэффициенте ai модели (8.1').

Выше выяснили смысл коэффициента детерминации R2 и пра­вило (12.9) его вычисления. Сейчас обратим внимание на то обстоятельство, что R2 вычисляется по выборочным данным

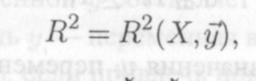12.15

а следовательно, является случайной переменной. По этой причине событие R²=0

которое может произойти, есть случайное событие (см. занятие 6). В то же время, если даже и оказывается справедливым желаемое неравенство R²˃0

то в силу опять-таки случайного характера величины R2 еще нет полного основания для отклонения гипотезы (12.12) или (12.14) о неудовлетворительной спецификации линейной модели (12.13). Нужен формализованный критерий (см. занятие 7) проверки гипо­тезы (12.14) против альтернативы Н1= Н0