Процедура точечного прогнозирования по оцененной линейной эконометрической модели значений эндогенной переменной

Пусть модель (13.1) оценена МНК по выборке 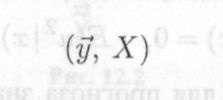(13.2)

в ситуации, когда все предпосылки теоремы Гаусса — Маркова адекватны. Таким образом, имеется оценка модели (13.1):

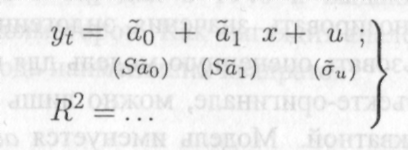13.3)

Обозначим символом xq значение экзогенной переменной дан­ной модели, при котором, по смыслу задачи, нужно вычислить прогноз значения эндогенной переменной. Прогноз обозначим сим­волом уо; в свою очередь, для наблюденного в реальности значения переменной у в ситуации, когда х = xq, будем использовать сим­вол у₀.

Заметим, что в рамках модели (13.1) пара (xq, уо) связана уравнением

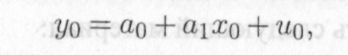(13.4)

где случайный остаток щ обладает, по предположению, количе­ственными характеристиками

т = Е(щ) = 0, Уа,г(щ) = а1.
Подчеркнем еще, что и величины, образующие выборку (13.2), связаны между собой уравнениями наблюдений (8.4), схемой Гаус­са — Маркова, аналогичными уравнению (13.4). Случайные остат­ки в этих уравнениях тоже имеют, по предположению, параметры (13.5)..

Ниже докажем (см. задачу 13.3), что в рамках модели (13.1) при наличии информации об объекте-оригинале в виде выборки (13.2) наилучший (в определенном смысле) точечный прогноз величины уо вычисляется по правилу

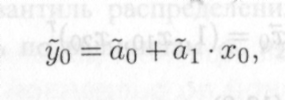(13.6)

т.е. в итоге подстановки в МНК-оценку функции регрессии моде­ли (13.1) значения х = xq экзогенной переменной. В свою очередь, средняя квадратическая (стандартная) ошибка прогноза (13.6) отыс­кивается (см. задачу 13.3 и следствие 1 к ней) по формуле

Sy₀ =o-_uy^/l + Qo, (13.7)

В задаче 13.1 покажем, что для модели парной регрессии (13.1) формулу (13.8) можно представить выразительнее:

13.10)

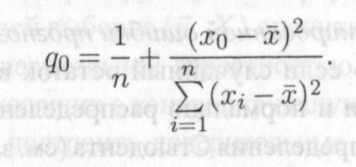
Из (13.10) видно, что точность прогноза (13.6) падает по мере удаления значения х₀ регрессора х от его выборочного среднего. Интуиция легко соглашается с этим фактом.

Обсужденная выше процедура точечного прогноза в рамках ли­нейной модели парной регрессии остается в силе и для линейной модели множественной регрессии (см. задачу 13.3). Так, например,

в рамках модели (8.1) с двумя регрессорами х\ и х₂ и гомоске-дастичном неавтокоррелированном остатком правило наилучшего точечного прогноза значения эндогенной переменной у₀ выглядит так:

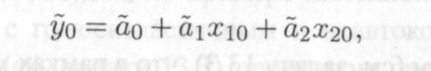(13.11)

где 1ю и Х2о — известные (заданные или наблюденные) значения регрессоров. Из них составим расширенный вектор известных значений регрессоров:

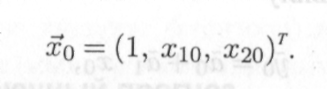13.12)

С ним формулы (13.7) и (13.8), позволяющие вычислить среднеква-дратическую (стандартную) ошибку прогноза (13.11) Sy₀, остаются справедливыми.