Дисперсии отклонений известны (метод взвешенных наименьших квадратов)

Данный метод применяется при известных для каждого наблюдений значений 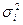. В этом случае можно устранить гетероскедастичность, разделив каждое наблюдаемое значение на соответствующее ему значение дисперсии. В этом суть метода взвешенных наименьших квадратов (ВМНК).

Для простоты рассмотрим взвешенный метод наименьших квадратов на примере парной регрессии 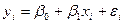. Разделим обе части 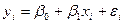на известное 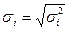: 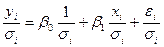. Обозначим , , 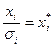, , 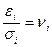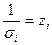получим уравнение регрессии без свободного члена, но с дополнительной объясняющей переменной 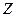и с преобразованным отклонением 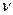, для которого выполняется условие гомоскедастичности: 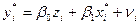. Таким образом ВМНК включает в себя следующие этапы:

1. Значения каждой пары наблюдений 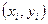делят на известную величину 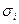. Тем самым наблюдениям с наименьшими дисперсиями придаются наибольшие веса, а с максимальными дисперсиями – наименьшие веса. Это увеличивает вероятность получения более точных оценок.
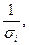
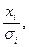
2. По методу наименьших квадратов для преобразованных значений ( 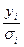) строится уравнение регрессии без свободного члена с гарантированными качествами оценок.