Тест Голдфелда-Квандта

В данном случае предполагается, что стандартное отклонение 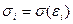пропорционально значению 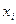переменной 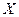в этом наблюдении, то есть .

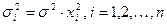Тест Голдфелда-Квандта состоит в следующем:

1. Все 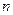наблюдений упорядочиваются по величине .

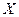2. Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей 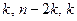соответственно.

3. Оцениваются отдельные регрессии для первой подвыборки (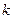 первых наблюдений) и для третьей подвыборки ( 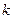последних наблюдений). Для парной регрессии Голдфелд и Квандт предлагают следующие пропорции: 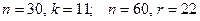. Если предположение о пропорциональности дисперсий отклонений значениям 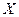верно, то дисперсия регрессии по первой подвыборке (рассчитываемая как 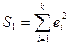) будет существенно меньше дисперсии регрессии по третьей подвыборке (рассчитываемой как ).

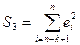4. Для сравнения соответствующих дисперсий строится соответствующая 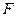-статистика: 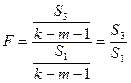. Здесь 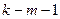- число степеней свободы соответствующих выборочных дисперсий ( 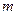- количество объясняющих переменных в уравнении регрессии). Построенная 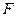-статистика имеет распределение Фишера с числом степеней свободы .

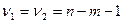5. Если 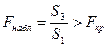(где 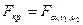, определяется по таблице, 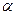- выбранный уровень значимости), то гипотеза об отсутствии гетероскедастичности отклоняется.

Критическое значение 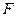- статистики рассчитывается с помощью функции MS Excel FРАСПОБР, в панели которой вводятся значения пороговой значимости (например, 0,05) и степени свободы .

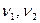Этот же тест может использоваться при предположении об обратной пропорциональности между 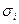и значениями объясняющей переменной. При этом статистика Фишера имеет вид: 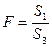. Для множественной регрессии данный тест обычно применяется для той объясняющей переменной, которая в наибольшей степени связана с 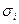. При этом 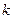должно быть больше, чем 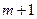. Если нет уверенности относительно выбора переменной 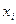, то данный тест может осуществляться для каждой из объясняющих переменных.