Прогнозирование в линейной модели регрессии

Первый случай. Если точно известны значения коэффициентов регрессии и дисперсия и даны (n+1) значения всех переменных, то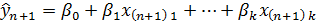

Второй случай. Точные значения коэффициентов регрессии и дисперсия неизвестны. Тогда в формуле прогноза они заменяются оценками, полученными по методу наименьших квадратов: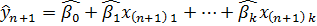

3. Линейная модель регрессии: коэффициент R²_, проверка значимости регрессии «в целом», проверка сложных гипотез о коэффициентах регрессии. Тест Чоу.

Коэффициент R²

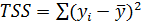- общая вариация зависимой переменной y;

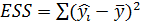– вариация зависимой переменной, объясненная регрессией;

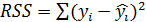- остаточная часть вариации зависимой переменной.

Для модели, в которую входит константа 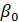выполняется равенство: TSS = ESS+RSS.

Коэффициент R² определяется как доля объясненной регрессией суммы квадратов зависимой переменной в общей сумме квадратов:

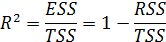
R² принадлежит [0; 1]. Коэффициент R² можно рассматривать как меру «качества подгонки» регрессионной модели: чем ближе значение R² к 1, тем «лучше качество подгонки» уравнения регрессии на выборочных данных.