2015-05-18
529
В рамках модели (1)
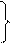
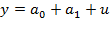
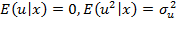
величины выборки (2)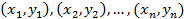 
связаны следующей системой линейных алгебраических уравнений:
……………………..
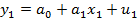
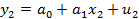
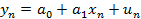
Она называется системой уравнений наблюдений объекта в рамках линейной модели (1), или, иначе, схемой Гаусса – Маркова. Компактная матричная запись:
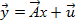
где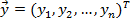 
– вектор наблюдения эндогенных перем-ых модели (1);
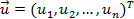- вектор случайных возмущений (остатков); 
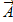- столбец параметров линейной модели
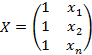– матрица коэф-тов при параметрах в системе уравнений наблюдений. наблюденных значений предопределенной переменной x модели (1), расширенная (при наличии в функции регрессии определяемого коэффициента 
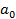) столбцом единиц;
Наконец,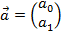 
- вектор неизвестных коэффициентов функции регрессии модели, подлежащий оцениванию по выборке (2).
