Расчет стандартных ошибок параметров уравнения парной регрессии и точности прогнозарования

Для расчета дисперсий D(a) и D(в) коэффициентов регрессии а и в в формулах (9) использовалась дисперсия σ² случайного члена ε. Эта дисперсия неизвестна, но ее можно оценить, используя выборочные данные. Можно доказать, что несмещенной оценкой дисперсии σ² является величина S², где:

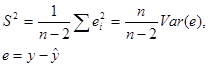(10)

Величина S называется стандартной ошибкой регрессии. Она служит мерой разброса зависимой переменной около линии регрессии. Запишем в формулах (9) дисперсию σ² ее оценкой S²:

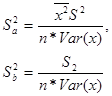(11)

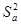и 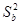называют оценками дисперсии коэффициентов регрессии, а величина Sa и Sв – стандартными ошибками коэффициентов регрессии. Они используются для построения доверительных интервалов, которым принадлежат параметры истинной регрессии и для проверки значимости коэффициентов регрессии.

Прогнозирование на основе эконометрических моделей является одной из основных задач эконометрики.

Под прогнозированием в эконометрике понимают построение оценки зависимой переменной для таких значений независимых переменных, которых нет в исходных наблюдениях.

Различают точечное прогнозирование и интервальное.

Точечный прогноз это число, значение зависимой переменной, вычисляемое для заданных значений независимых переменных.

Интервальный прогноз это интервал, в котором с заданным уровнем значимости (с заданной вероятностью) находится истинное значение зависимой переменной для заданных значений независимых переменных.

Рассмотрим парную линейную регрессионную модель 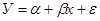и соответствующее выборочное уравнение регрессии 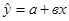. Обозначим через у_р истинное значение переменной у для заданного значения независимой переменной х_р, т.е. .

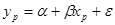Точечным прогнозом для у_р является 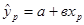, т.е. чтобы получить точечный прогноз нужно в построенное уравнение регрессии подставить заданное значение независимой переменной.

Ошибкой предсказания (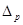) называют разность между прогнозным и истинным значениями независимой переменной.

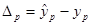
Можно доказать, что дисперсия ошибки предсказания

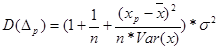. (21)

Из (21) следует, что чем ближе заданное значение независимой переменной 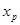к 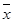тем меньше дисперсия прогноза и чем больше объем выборки n, тем меньше дисперсия прогноза.

Заменив в (21) дисперсию 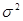на ее оценку 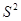, извлечем, квадратный корень и получим стандартную ошибку предсказания .

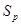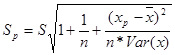(22)

Выберем уровень значимости α и по таблице распределения Стьюдента найдем t_кр. Тогда с вероятностью 1- α истинное значение переменной у_р будет находится внутри интервала:

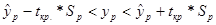(23)

Очевидно, что чем ближе 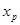к 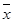и чем больше n, тем уже доверительный интервал (тем точнее прогноз). Это надо учитывать, выбирая прогнозные значения для независимой переменной.