Вернемся к задаче оценки параметров уравнения парной регрессии и решим ее с помощью процедур, сформулированных в теореме Гаусса-маркова.
Имеем уравнени парной линейной регрессии:
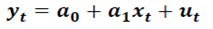
Выборку наблюдений объемом n за поведением экономического объекта
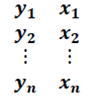
Сформулируем необходимые вектора и матрицу коэффициентов уравнений наблюдений:

Столбец из единиц появился в матрице, в связи с тем, что в спецификации присутствует параметр 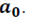

Вот все необходимое для оценки модели
Выражение 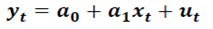 позволяет вычислить оценки параметров. Для этого вначале вычисляется произведение матриц:
позволяет вычислить оценки параметров. Для этого вначале вычисляется произведение матриц:
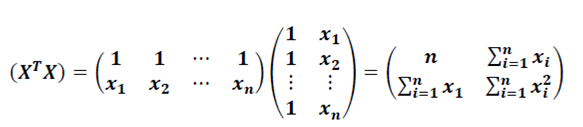
Матрица обратная к этой есть
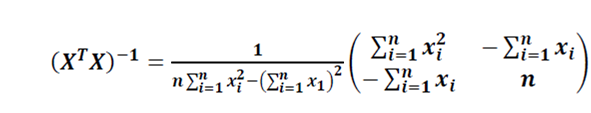
Вычисляется произведение
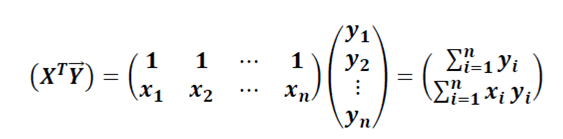
Подставляя выражение в последние два произведения в исходное выражение получим вектор оценок параметров линейной модели парной регресии
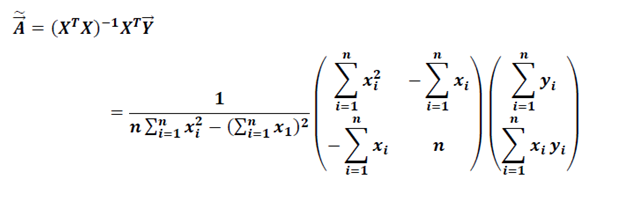
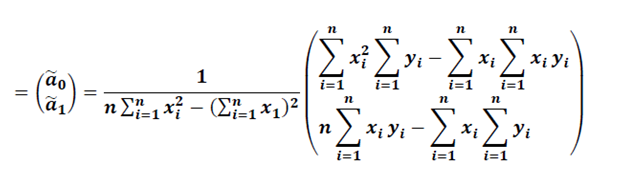
 2015-05-18
2015-05-18 842
842








