Проверка статистических гипотез является одной из основных задач математической статистики.
Объективной основой проверки истинности/ложности статистической гипотезы 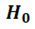 о случайно переменной может служить только ее значения, полученные в результате наблюдений.
о случайно переменной может служить только ее значения, полученные в результате наблюдений.
Порядок действий при проверке статистических гипотез можно представить в виде след алгоритма:
Шаг 1. Формулируется основная статистическая гипотеза. Формулировка делается, как в описательной форме так и в математическом виде
Шаг 2. Искусственно созадется случайная переменная z, тесто связанная с выдвинутой гипотезой и известным законом распределения 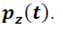 Закон распределения случайной переменной, которая содержится в сформулированной основной гипотезе, может быть неизвестен, а, следовательно, ничего нельзя сказать о ее поведении. Поэтому создается случайная переменная, о поведении которой можно судить по ее закону распределения.
Закон распределения случайной переменной, которая содержится в сформулированной основной гипотезе, может быть неизвестен, а, следовательно, ничего нельзя сказать о ее поведении. Поэтому создается случайная переменная, о поведении которой можно судить по ее закону распределения.
Шаг 3. Задается значение доверительной вероятности 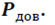
Областро определения созданной случайной переменной z разбивается на две непересекающихся области: область, где выдвинутая гипотеза 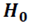 принимается
принимается 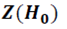 , и область, где основная гипотеза отклоняется
, и область, где основная гипотеза отклоняется 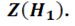
Разбиение области определения созданной случайно переменной осуществляется таким образом, чтобы оказалось справедливым равенство:
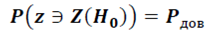
Шаг 4. Проверяется появление случайного события 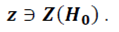 если событие появилось, то гипотеза
если событие появилось, то гипотеза 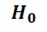 принимается как непротиворечащая опытным данным, если оно не появилось, то гипотеза
принимается как непротиворечащая опытным данным, если оно не появилось, то гипотеза 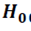 отклоняется
отклоняется
Случайную переменную z называеют статистикой критерия гипотезы 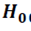 .
.
 2015-05-18
2015-05-18 1084
1084








