Методы устранения автокорреляции в уравнениях множественной регрессии

Рассмотрим два последовательных уравнения наблюдения 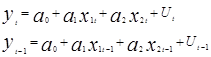. Умножим уравнение второе уравнение на ρ и вычтем из первого: 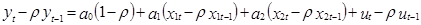. Учитывая, что u_t-ρu_t-1=ε_t и делая замену переменных: 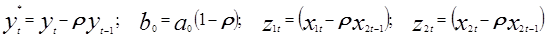получим систему уравнений, в которых дисперсия случайных возмущений постоянна: 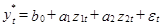. Параметры полученного уравнения можно оценить с помощью МНК. Если значение ρ известно, то решение окончено. Замечание:Уравнения имеют смысл при t=2, т.к. при t=1 оно не может быть получено. Для включения первого уравнения наблюдений в систему его умножают на (1-ρ)^½. Этот множитель (поправка Прайса-Уинстона) обеспечивает уменьшение влияния первого уравнения на все остальные при ρ близких к единице. Тогда окончательно система уравнений наблюдений принимает вид: Замечание: Рассмотренный прием справедлив, если известен коэффициент корреляции между последовательными случайными возмущениями. На практике, как правило, он неизвестен. При неизвестном значении коэффициента корреляции применяется итерационная процедура метода последовательных приближений. Этот метод получил название процедура Кохрейна-Оркатта: Задается число 0< 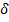< 1. 1) Значению коэффициента корреляции присваивается значение p₀ =0. 2) По имеющейся выборке оцениваются значения параметров модели и значения случайных возмущений (u₁, u₂,…,u_n)по системе уравнений наблюдений. 3) По массиву случайных возмущений (u₁, u₂,…,u_n) оценивается модель u_t =pu_t-1 + ɛ_t. 4) Получается значение p₁, которое сравнивается с предыдущим значением коэффициента детерминации. 5) Если выполняется условие 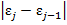≤ 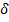, то процесс поиска параметров прекращается. В противном случае переменной p₀ присваивается значение p₁, и повторяются шаги 2, 3, 4.