Проблема гетероскедастичности модели. Критерии её диагностики

Проблема гетероскедастичности возникает, когда наблюдения за эконометрическими переменными, включенными в модель, таковы, что точность наблюдений, проведенных в различные моменты времени, неодинакова, другими словами:

.

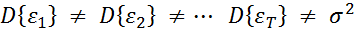Различают явную и неявную гетероскедастичность. Явная гетероскедастичность возникает, когда шоковая переменная модели имеет различные дисперсии в различные моменты наблюдения правильно специфицированной модели. В общем виде перепишем модель для случая двух экзогенных переменных:

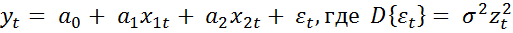
Здесь 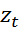– так называемый фактор пропорциональности, на практике 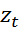выбирается как некоторая экзогенная переменная.

Неявная гетероскедастичность возникает вследствие неправильной спецификации модели.

Критерий Парка.

1. С помощью МНК оценивают параметры модели и рассчитывают отклонения: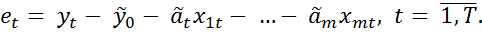

2. Применяют полученные отклонения 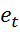для построения вспомогательной модели: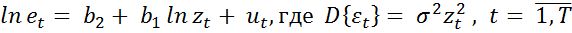

3. Производят проверку значимости параметров вспомогательной модели по критерию Стьюдента. При получении вывода о значимости параметров диагностируют наличие гетероскедастичности.

Критерий Голдфилда – Кандта.

1. Упорядочивают наблюдения за эндогенной переменной в соответствии с величиной фактора z: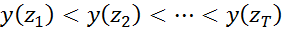

2. Разбивают выборку на три части объемами: 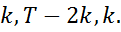Образуют вспомогательную регрессию, образованную из 1-й и 3-й частей упорядоченной выборки, рассчитывают остатки: RSS(3), RSS(1).

3. Применяют F-критерий с решающей функцией вида:

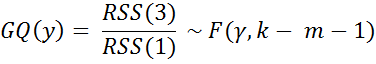
Если расчетное значение величины 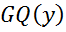превышает табличное, то делают вывод о наличии гетероскедантичности.

Критерий Бриша-Пагана.

1 и 2 совпадают с критерием Парка, где учитывают .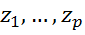

3. Гипотезу значимости параметров вспомогательной регрессии 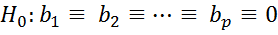осуществляют на основе решающей функции:

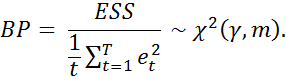
Если расчетное значение статистики 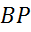превышает табличное значение из таблиц 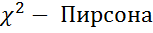, то делают вывод о наличии гетероскедантичности.

Критерий Вайта. Не требует задания фактора пропорционал .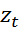

1. Вычисляют остатки исходного эконометрического уравнения .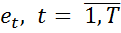

2. Образовывают вспомогательную модель:

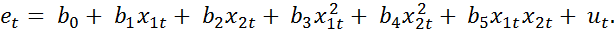
3. Осуществляют МНК-оценивания регрессии, полученной на предыдущем шаге, и проверяют значимость ее параметров по правилу: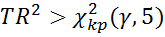

При подтверждении данного неравенства делают вывод о наличии гетероскедастичности.