Свойства:
1) МНК-оценки вектора параметров МЛР обладают свойством несмещенности: M{  } =
} = 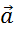
2)Несмещённая оценка дисперсии для случайной переменной ε:
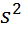 =
= 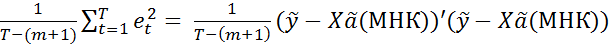 .
.
3) Дисперсия МНК-оценок параметров aj имеет вид: 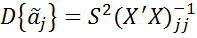 , где
, где 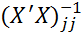 - диагональный элемент, стоящий на пересечении j-й строки и j-го столбца
- диагональный элемент, стоящий на пересечении j-й строки и j-го столбца
4) t-статистики для определения значимости параметров aj имеют вид: 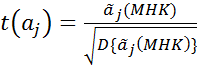 Если |t(
Если |t(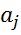 )|>
)|> 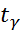 , где
, где 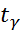 - квантиль распределения Стьюдента с надёжностью γ, то отклоняют гипотезу
- квантиль распределения Стьюдента с надёжностью γ, то отклоняют гипотезу 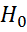 и делают вывод о существенной значимости параметра
и делают вывод о существенной значимости параметра 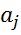 .
.
5) Доверительные интервалы параметров aj имеют вид:
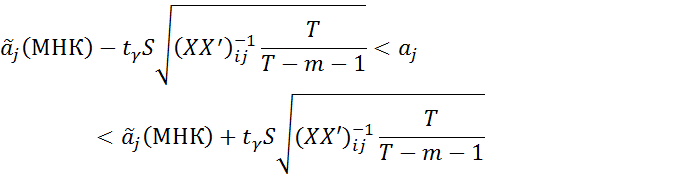
6) Адекватность МЛР проверяется с помощью F-критерия:Если 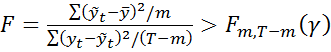 , то гипотезаH0: a1 = a2 = …= am = 0неверна.
, то гипотезаH0: a1 = a2 = …= am = 0неверна.
Теорема Гаусса-Маркова:Фундаментальное свойство МНК: МНК-оценки параметров линейной регрессии обладают наименьшими дисперсиями среди множества всех несмещённых и линейно-зависимых от энд.переменных оценок в рамках модельных предположений П1-П4.
МЛР с линейными ограничениями на параметры:
Y=Xa+ε, Ba=b (ЛОГ), B – заданная матрица полного ранга rank B=k, 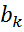 – заданный вектор размерности k.
– заданный вектор размерности k.
Частные случаи ЛОГ:
1) 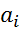 =0, B=(0…010…0), b=0
=0, B=(0…010…0), b=0
2)два параметра совпадают 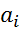 =
= 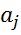 , B=(0…010…-10…0), b=0
, B=(0…010…-10…0), b=0
3)сумма нескольких параметров равна 1
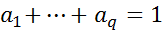 , q>1, B=(01…10…0), b=0
, q>1, B=(01…10…0), b=0
4)подмножество коэффициентов вектора параметров а равно 0
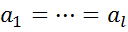 =0, k=l, B=
=0, k=l, B= 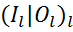 , b=
, b= 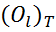 .
.
Оценка параметров с учётом ЛОГ:
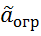 (МНК) =
(МНК) = 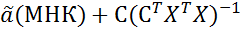 (b-B
(b-B 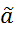 ),
),
C=(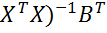 ,
, 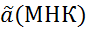 =(
=(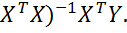
 2015-05-18
2015-05-18 541
541








