Идентификация модели регрессии

Построение эконометрической модели — центральная проблема любого эконометрического исследования, поскольку ее «качество» определяет достоверность и обоснованность результатов анализа тенденций развития, прогнозов рассматриваемых социально-экономических процессов, а также вытекающих из них выводов, в том числе и по вопросам разработки необходимых управленческих мероприятий.

В эконометрических исследованиях обычно предполагается, что закономерности моделируемого процесса складываются под влиянием других явлений, факторов. В зависимости от количества факторов, включенных вуравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными — у и х, т. е. модель вида

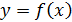где у — зависимая переменная (результативный признак);

х — независимая, или объясняющая, переменная (признак-фактор).

Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида

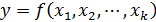Любое эконометрическое исследование начинается с идентификацией модели регрессии, целями которой являются:

1. Выбор рационального состава включаемых в модель переменных и определение количественных характеристик, отражающих их уровни в прошлые периоды времени (на однородных объектах некоторой совокупности — территориях, предприятиях и т.п.).

2. Обоснование типа и формы модели (спецификация модели регрессии), выражаемой математическим уравнением, связывающим включенные в модель факторные и результативные признаки.

Прежде всего, из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Предположим, что выдвигается гипотеза о том, что величина спроса у на товар А находится в обратной зависимости от цены х, т. е. 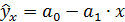. В этом случае необходимо знать, какие остальные факторы предполагаются неизменными, возможно, в дальнейшем их придется учесть в модели и от простой регрессии перейти к множественной.

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений. Так, если зависимость спроса у от цены х характеризуется, например, уравнением 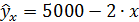, то это означает, что с ростом цены на 1 д. е. спрос в среднем уменьшается на 2 д. е. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией:

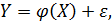
где 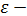случайная величина, характеризующая отклонение от функции регрессии. Эту переменную будем называть возмущающей или просто возмущением. Таким образом, в регрессионной модели зависимая переменная Y есть некоторая функция 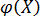с точностью до случайного возмущения .

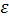Рассмотрим линейный регрессионный анализ, для которого функция 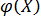линейна относительно оцениваемых параметров:

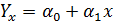. (3.3)

Предположим, что для оценки параметров линейной функции регрессии (3.3) взята выборка, содержащая n пар значений переменных 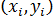, где 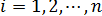. В этом случае линейная парная регрессионная модель имеет вид:

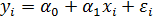. (3.4)

Отметим основные предпосылки регрессионного анализа:

1. В модели (3.4) возмущение 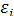(или зависимая переменная 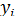) есть величина случайная, а объясняющая переменная 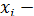величина неслучайная.

2. Математическое ожидание возмущения 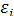равно нулю:

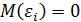. (3.5)

(или математическое ожидание зависимой переменной равно линейной функции регрессии: ).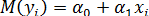

3. Дисперсия возмущения 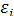(или зависимой переменной 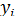) постоянна для любого i:

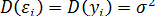. (3.6)

4. Возмущения 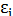,и 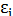(или переменные 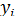и 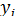) не коррелированы:

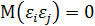
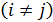. (3.7)

5. Возмущение 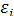(или зависимая переменная 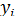) есть нормально
распределенная случайная величина.

Для получения уравнения регрессии достаточно первых четырех предпосылок. Требование выполнения пятой предпосылки (т.е. рассмотрение «нормальной регрессии») необходимо для оценки точности уравнения регрессии и его параметров.

Оценкой модели (3.4) по выборке является уравнение регрессии

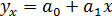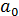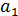. Параметры этого уравнения и определяются на основе метода наименьших квадратов.

Случайная величина 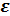включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

Приведенное ранее уравнение зависимости спроса у от цены х точнее следует записывать как

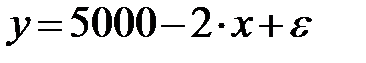
ибо всегда есть место для действия случайности. Обратная зависимость спроса от цены не обязательно характеризуется линейной функцией

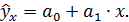
Возможны и другие соотношения, например:

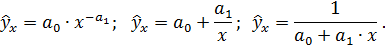
Поэтому от правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере модельные значения результативного признака 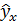подходят к фактическим данным у.

К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для у_х, но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. Так, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения.

Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне. Так, в исследованиях спроса и потребления в качестве объясняющей переменной широко используется «доход на душу населения». Вместе с тем статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например в результате наличия сокрытых доходов.

Приведем еще один пример: в настоящее время органы государственной статистики получают балансы предприятий, достоверность которых никто не подтверждает. Последующее обобщение такой информации может содержать ошибки измерения. Исследуя, например, в качестве результативного признака прибыль предприятий, мы должны быть уверены, что предприятия показывают в отчетности адекватные реальной действительности величины.

Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции 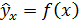может быть осуществлен тремя методами:

• графическим;

• аналитическим, т. е. исходя из теории изучаемой взаимосвязи;

• экспериментальным.

При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. В этом случае строят график при этом по осям 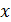и y в масштабе откладывают их значения в результате на плоскости получают 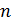точек. Совокупность этих точек называют полем корреляции. По полю корреляции проводят аппроксимирующую кривую, по которой и производят выбор функции регрессии.

Основные типы кривых, используемые при количественной оценке связей между двумя переменными:

;

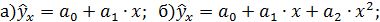
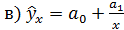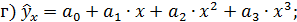
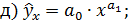
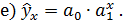
Класс математических функций для описания связи двух переменных достаточно широк. Кроме уже указанных используются и другие типы кривых:

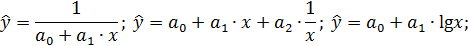
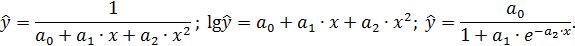
Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.

Пусть, например, изучается потребность предприятия в электроэнергии у в зависимости от объема выпускаемой продукции х.

Все потребление электроэнергии у можно подразделить на две части:

• не связанное с производством продукции ;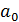

• непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее с увеличением объема выпуска .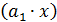

Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида

.

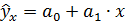Если затем разделить обе части уравнения на величину объема выпуска продукции (х), то получим выражение зависимости удельного расхода электроэнергии на единицу продукции 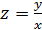от объема выпущенной продукции (х) в виде уравнения равносторонней гиперболы:

.

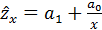Аналогично затраты предприятия могут быть подразделены на условно-переменные, изменяющиеся пропорционально изменению объема продукции (расход материала, оплата труда и др.) иусловно-постоянные, не изменяющиеся с изменением объема производства (арендная плата, содержание администрации и др.). Соответственно зависимость затрат на производство (у) от объема продукции (х) характеризуется линейной функцией:

,

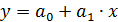а зависимость себестоимости единицы продукции (z) от объема продукции — равносторонней гиперболой

.

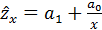При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии 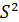, рассчитанной при разных моделях.

Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии 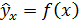,то фактические значения результативного признака совпадают с модельными 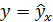,т. е. они полностью обусловлены влиянием фактора 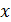. В этом случае остаточная дисперсия 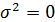. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Воздействие неучтенных случайных факторов в модель регрессии определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии 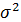. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия:

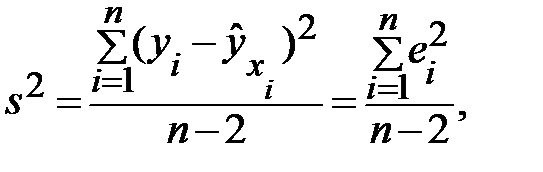(3.5)

где 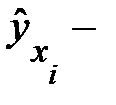модельное значение результативного признака, найденное по уравнению регрессии;

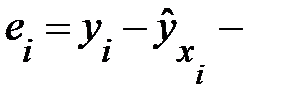выборочная оценка возмущения 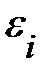или остаток регрессии.

В знаменателе выражения (3.5) стоит число степеней свободы 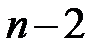, а не 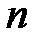, так как две степени свободы теряются при определении двух параметров прямо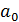й и .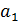

Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих не учитываемых в уравнении регрессии факторов лучше уравнение регрессии подходит к исходным данным. При обработке статистических данных на компьютере перебираются разные математические функции в автоматическом режиме и из них выбирается та, для которой остаточная дисперсия является наименьшей.

Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдается более простым видам функций, ибо они в большей степени поддаются интерпретации и требуют меньшего объема наблюдений. Результаты многих исследований подтверждают, что число наблюдений должно в 6 — 7 раз превышать число рассчитываемых параметров при переменной х. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при д: должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени

,

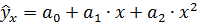то требуется объем информации уже не менее 14 наблюдений. Учитывая, что эконометрические модели часто строятся по данным рядов динамики, ограниченным по протяженности (10, 20, 30 лет), при выборе спецификации модели предпочтительна модель с меньшим числом параметров при х.