Ранговая корреляция

До сих пор мы анализировали зависимости между количественными переменными. Однако на практике часто встречаются с необходимостью изучения связи между качественными признаками. В этих условиях могут быть использованы и другие показатели для определения степени тесноты связи.

Элементарной характеристикой степени тесноты связи является коэффициент Фехнера:

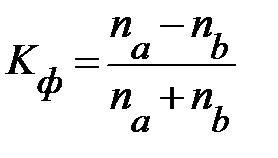, (2.24)

где 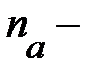количество совпадений знаков отклонений индивидуальных величин факторного признака 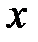и результативного признака 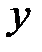от их средней арифметической величины (например, «плюс» и «плюс», «минус» и «минус», «отсутствие отклонения» и «отсутствие отклонения»); 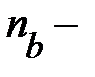количество несовпадений знаков отклонений индивидуальных значений изучаемых признаков от значения их средней арифметической.

Коэффициент Фехнера целесообразно использовать для установления факта наличия связи при небольшом объеме исходной информации. Он изменяется в пределах .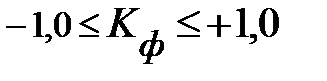

Пример 2.3. По группе однородных предприятий имеются данные об объеме выпущенной продукции и уровне механизации трудоемких и тяжелых работ:

№ предприятия	Уровень механизации трудоемких и тяжелых работ, %	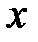Объем продукции, млн. руб.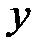

Требуется оценить степень тесноты связи между показателями механизации трудоемких и тяжелых работ и объемом продукции при помощи коэффициент Фехнера.

Предварительно вычислим среднеарифметические значения признаков:

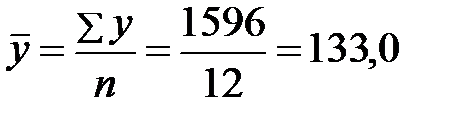млн. руб.;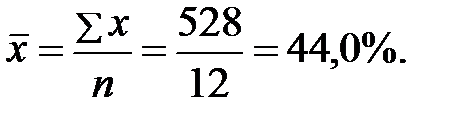

Для расчета коэффициента Фехнера составляется вспомогательная таблица, которая имеет вид:

Уровень механизации работ, %	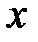	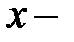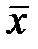Объем продукции, млн. руб.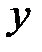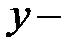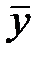
	-22 - 8 -23 - 4 - 5 - 5 -13 - 8		-16 -47 -21 -81 - 1 -13 -27

Коэффициент Фехнера вычислим по формуле (3.24):

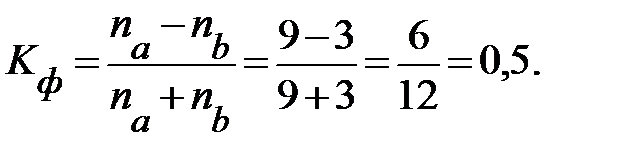
Полученное значение коэффициента свидетельствует о наличии связи между уровнем механизации работ и объемом продукции.

Для определения тесноты связи как между количественными, так и между качественными признаками, при условии, что значения этих признаков могут быть проранжированы по степени убывания или возрастания, используется ранговый коэффициент корреляции Спирмена:

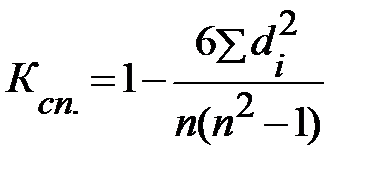, (2.25)

где 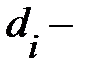разность между величинами рангов признака – фактора и результативного признака; 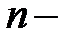число показателей (рангов) изучаемого ряда.

Он варьирует в пределах от – 1,0 до + 1,0.

При проверке значимости 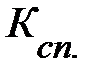исходят из того, что в случае справедливости нулевой гипотезы об отсутствии корреляционной связи между переменными статистика

имеет 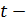распределение Стьюдента с 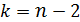степенями свободы. Поэтому 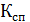значим на уровне 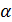, если фактически расчетное значение 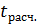будет больше критического, т. 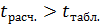е. , где 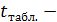табличное значение 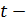критерия Стьюдента, определенное на уровне значимости 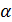при числе степеней свободы .

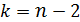Пример 2.4. По группе акционерных коммерческих банков региона имеются следующие данные:

№ банка	Активы банка, млн. руб. x	Прибыль, млн. руб. y
		39,6 17,8 12,7 14,9 4,0 15,5 6,4 10,1 3,4 13,4

Исчислить ранговый коэффициент корреляции Спирмена для оценки тесноты связи между суммой прибыли и размером его активов.

Решение

Для расчета коэффициента корреляции рангов предварительно выполняется ранжирование банков по уровню каждого признака (табл. 2.4).

Таблица 2.4

№ банка	Активы банка, млн. руб.	Ранг по x	№ банка	Прибыль, млн. руб.	Ранг по y
				3,4 4,0 6,4 10,1 12,7 13,4 14,9 15,5 17,8 39,6

Дальнейшие расчеты приведем в табл. 2.5.

Таблица 2.5

Расчет коэффициента корреляции рангов

№ п/п	Активы банка, млн. руб. x	Прибыль, млн. руб. y	Ранги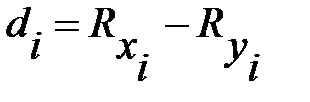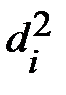
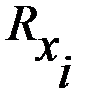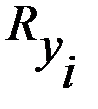		39,6 17,8 12,7 14,9 4,0 15,5 6,4 10,1 3,4 13,4			-1 -2 -6
Итого	-	-	-	-

На основании данных табл. 2.5 по формуле (2.25) получим коэффициент корреляции рангов:

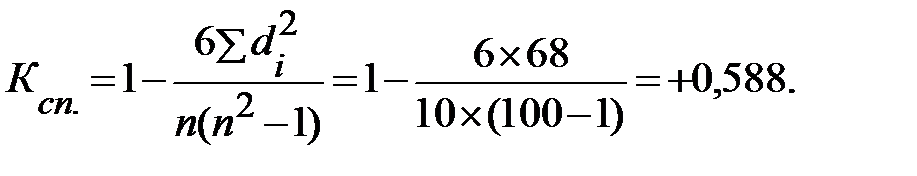
Для проверки значимости 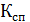по формуле (2.26) вычислим

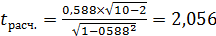и найдем по таблицам теории вероятностей критическое значение 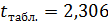. Так как , поэтому общий вывод по результатам анализа: есть необходимость увеличивать объем выборки.

Для исследования степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, может быть использован коэффициент ассоциации Д. Юла или коэффициент контингенции К. Пирсона.

Расчетная таблица в этом случае состоит из четырех ячеек («таблица четырех полей»), статистическое сказуемое которой схематически может быть представлено в следующем виде:

Признак	А (да)	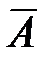(нет)	Итого
В (да)	a	b	a+b
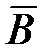(нет)	c	d	c+d
Итого	a+c	b+d	n

В расчетной таблице:

a, b, c, d – частоты взаимного сочетания (комбинации) двух альтернативных признаков – A – 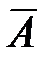и B – 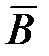; n – общая сумма частот.

Коэффициент ассоциации исчисляется по формуле:

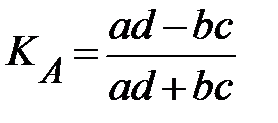. (2.27)

Коэффициент контингенции:

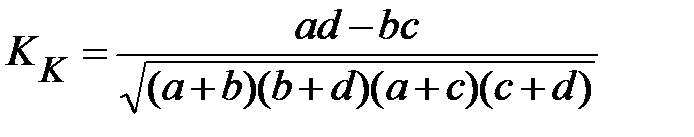, (2.28)

где 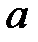, , 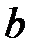, 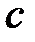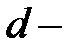числа в четырехклеточной таблице.

Коэффициент контингенции также изменяется от – 1,0 до + 1,0, но всегда его величина для тех же данных меньше коэффициента ассоциации.

Пример 2.5. В результате обследования работников предприятия получены следующие данные (чел.):

Образование	Удовлетворены своей работой	Не удовлетворены своей работой	Итого
Высшее и среднее
Незаконченное среднее
Итого

Решение

Коэффициент ассоциации –

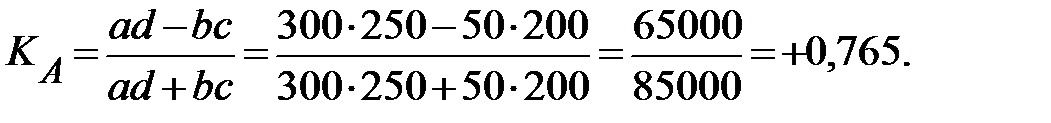
Коэффициент контингенции –

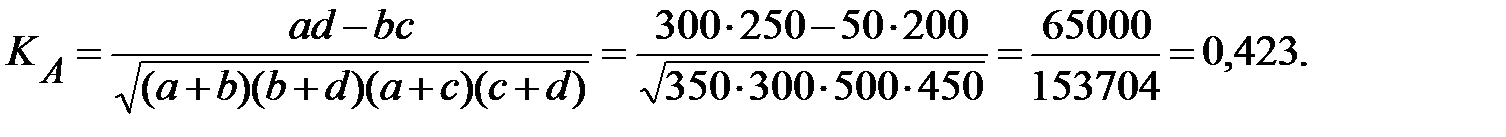
Полученные коэффициенты подтверждают наличие существенной связи между исследуемыми признаками. Однако коэффициент контингенции всегда бывает меньше коэффициента ассоциации и дает более корректную оценку тесноты связи.