Понятие о многомерном корреляционном анализе

Экономические явления чаще всего адекватно описываются многофакторными моделями. Поэтому возникает необходимость обобщить рассмотренную выше двумерную корреляционную модель на случай нескольких переменных.

Пусть имеется совокупность случайных переменных 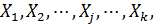имеющих совместное нормальное распределение. В этом случае матрицу

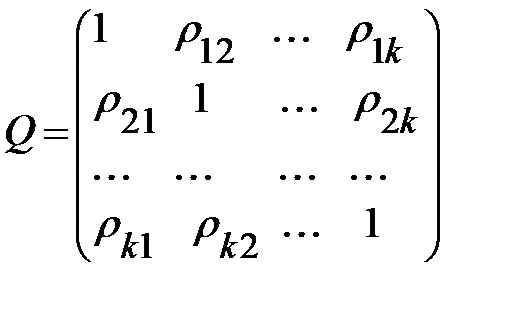, (2.11)

определяемых по формуле (2.1), будем называть корреляционной. Основная задача многомерного корреляционного анализа состоит в оценке корреляционной матрицы по выборке. Эта задача решается определением матрицы выборочных коэффициентов корреляции:

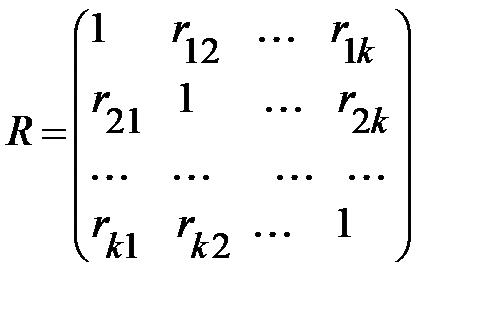, (2.12)

где 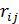выборочный парный коэффициент корреляции, рассчитываемый по общей формуле:

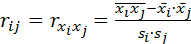. (2.13)

В многомерном корреляционном анализе рассматривают две типовые задачи:

а) определение тесноты связи между переменными при фиксировании или исключении влияния остальных l переменных, где ;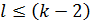

б) определение тесноты связи одной переменной с совокупностью остальных переменных, включенных в модель.

Эти задачи решаются с помощью частных и множественных коэффициентов корреляции.

Частные коэффициент корреляции. Если переменные коррелируют друг с другом, то на величине парного коэффициента корреляции частично сказывается влияние других переменных. В связи с этим часто возникает необходимость исследовать частную корреляцию между переменными при исключении (элиминировании) влияния одной или нескольких других переменных.

Выборочный частный коэффициент корреляции между переменным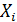и и 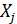при фиксированных значениях остальных 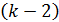переменных оценивается выражением:

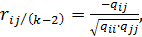(2.14)

где 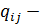алгебраические дополнения к элементу 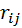корреляционной матрицы R; 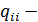алгебраические дополнения к элементу 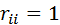; 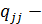алгебраические дополнения к элементу .

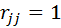Необходимо заметить, что в формуле (2.14) 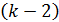указывает на то, что из модели исключено влияние 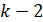факторов на факторы 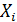и .

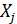Множественный коэффициент корреляции. Теснота линейной взаимосвязи одной переменной 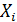с совокупностью других 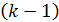переменных 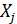, рассматриваемой в целом, измеряется с помощью множественного коэффициента корреляции. Выборочный множественный коэффициента корреляции например между 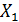и остальными 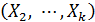определяется выражением:

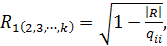(2.15)

где 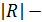определитель матрицы выборочных коэффициентов корреляции (2.12); 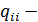алгебраические дополнения к элементу .

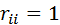Можно показать, что множественный выборочный коэффициент корреляции значимо отличается от нуля, если значение статистики

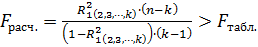, (2.16)

где 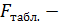табличное значение F – критерия Фишера на уровне значимости 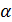при числе степеней свободы 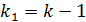и .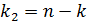

Рассмотрим частный случаи трехмерной генеральной сово­купности (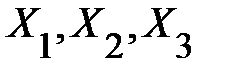) понятия и правила вычисления частных и мно­жественных коэффициентов корреляции. Пусть каждый экономи­ческий объект, элемент генеральной совокупности характеризует­ся тремя показателям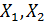и и 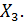Требуется по данным выборки объемом п из генеральной совокупности исследовать взаимосвязь между этими показателями.

В этом случае выборка объемом п будет представлять собой выборочную мат­рицу наблюдений X:

.

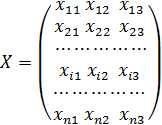В ней каждая i-я строка (i = 1, 2,..., k)характеризует i -и эконо­мический объект, а столбец, например первый, содержит значение для 1-го показателя для всех п объектов.

Для трехмерной (и других многомерных) корреляционных моделей важную роль играют частные и множественные коэффициенты корреляции или детерминации (коэффициент детерминации равен квадрату соответствующего коэффициента корреляции). Частные и множественные коэффициенты корреляции рассчитываются на основе выборочных парных коэффициентов корреляции.

Частные коэффициенты корреляции рассчитываются на основе выборочных парных коэффициентов корреляции. Для трехмерных моделей расчетные формулы таковы:

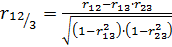; (2.17)

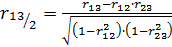: (2.18)

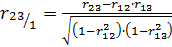. (2.19)

Таким образом, для анализа взаимосвязи между двумя признаками в трехмерных и многомерных моделях мы имеем по два коэффициента корреляции. Например, парный r₁₂ и частный r_12/3которые характеризуют степень линейной зависимости между величинам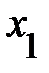и и 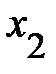.Однако если парный коэффициент r₁₂ оценива­ет степень зависимости на фоне влияния 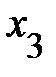, то частный коэффици­ент корреляции r_12/3 - при исключенном влиянии .

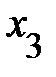Следовательно, частный коэффициент корреляции более точно характеризует степень линейной зависимости.

Частный коэффициент корреляции обладает всеми свойствами парного, т.е. изменяется в пределах от-1 до+1. Если частный ко­эффициент корреляции равен ±1, то связь между двумя величинами функциональная, а равенство его нулю свидетельствует о линейной независимости этих величин. Частный коэффициент корреляции, вычисленный на основе выборки объемом n, имеет такое же распределение, что и парный коэффициент корреляции. Поэтому значимость частного коэффициента

корреляции оценивают так же, как и парного коэффициент корреляции. Для оценки значимости вычисляют расчетное значение t – статистики Стьюдента:

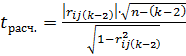. (2.20)

Если 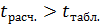, то частный коэффициент корреляции значимо отличается от нуля.

Множественный коэффициент корреляции тоже получаются на основании выборочных коэффициентов корреляции. Для трехмерной модели множественные коэффициенты корреляции вычисляются по формулам:

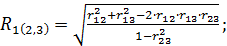(2.21)

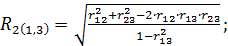(2.22)

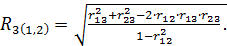(2.23)

Множественный коэффициент корреляции, например 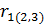, харак­теризует степень линейной зависимости между величиной 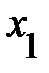, и ос­тальными переменными (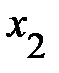, 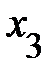), входящими в модель. Он изменяет­ся в пределах от 0 до 1. Равенство его единице свидетельствует о функциональной зависимости между, например, 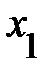, и остальными переменными (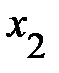, 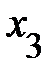), входящими в модель, а равенство его 0 свиде­тельствует об отсутствии линейной зависимости между 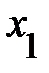, и пере­менными (, ).

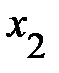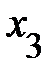Квадрат коэффициента корреляции называют коэффициентом детерминации. При этом множественный коэффициент детермина­ции, например 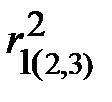, характеризует долю дисперсии 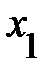объясняемую влиянием показателе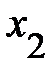й и 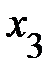. Например, если 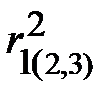= 0,85, то это сви­детельствует, что 85% дисперсии 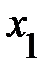объясняется влиянием показателе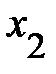й и 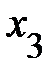, а 15% дисперсии 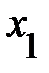объясняется влиянием факторов, которые не вошли в модель.

Таким образом, коэффициент детерминации характеризует долю дисперсии одной величины, например у, объясняемой влия­нием фактора .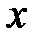

Рассмотрим пример.

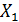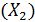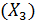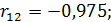
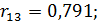
Пример 2.2. Для исследования зависимости между прибылью , затратами на 1 руб. произведенной продукции и стоимостью основных фондов была проведена выборка из 100 предприятии одной отрасли. Вычисленные парные коэффициенты корреляции оказались значимыми и составили: 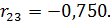Вычислить частные и множественные коэффициенты корреляции и оценить их значимость на уровне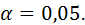

Решение. По формуле (3.17) вычислим частный коэффициент корреляции:

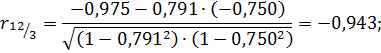
и аналогично ; .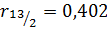

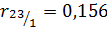Оценим значимость 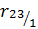. Расчетное значение критерия Стьюдента получим по формуле (3.20):

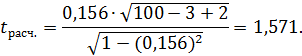
По таблице распределения Стьюдента находим 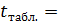1,99. Так как , то частный коэффициент корреляции 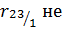значимо отличается от нуля.

Теперь оценим значимость 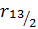. Для этого получим расчетное значение критерия Стьюдента:

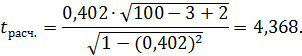
Так как 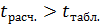, то частный коэффициент корреляции 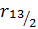значим. Тем более значим, будет коэффициент 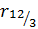, так как .

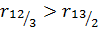Сравнивая значения парного 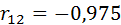и частного 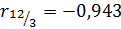коэффициентов корреляции (они достаточно близки), мож­но утверждать, что 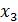слабо влияет на степень зависимости между величинам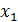и и .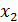

С другой стороны сравнивая частные коэффициенты корреляции соответствующими парными коэффициентами корреляции, видим, что за счет «очищения связи» наибольшему изменению подвергся коэффициент корреляции между затратами на 1руб. произведенной продукции и стоимостью основных фондов (изменилась не только его величина, но даже и знак: 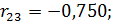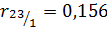). Можно утверждать также, что между прибылью 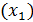и затратами на 1 руб. произведенной продукции 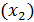существует сильная обратная корреляционная связь 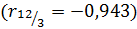. Если же устранить влияние переменной «затраты на 1 руб. произведенной продукции» 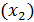, то в чистом виде на прибыл 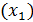слабо влияет на стоимость основных фондов 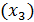. Наконец если устранить влияние прибыли 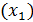, на затраты на 1 руб. произведенной продукции 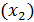и на стоимость основных фондов 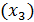то связь между затратами на 1 руб. произведенной продукции и стоимостью основных фондов практически отсутствует т. к. .

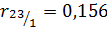Определим теперь множественный коэффициент корреляции по формулам (2.21), (2.22) и (2.23) соответственно:

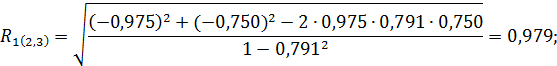
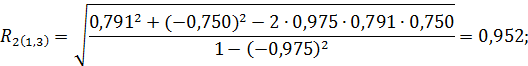
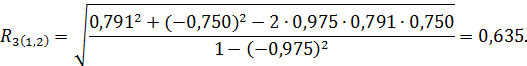
Оценим значимость 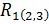. Для этого по формуле (3.16) вычислим расчетное значение критерия Фишера:

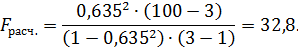
По таблице 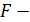распределения Фишера находим 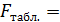8,56. Так как 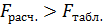, то множественный коэффициент корреляции 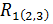значим. Тем более будут значимы большие коэффициенты 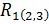и .

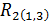Множественный коэффициент корреляции 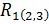свидетельствует о том, что между прибылью, с одной стороны, и затратами на 1 руб. произведенной продукции и стоимостью ос­новных фондов – с другой, существует сильная связь. Рассчитаем множественный коэффициент детерминации:

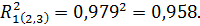
Множественный коэффициент детерминации 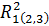показывает, что изменение (вариация) прибыли 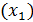предприятии на 95,8% объясняется изменением затрат на 1 руб. произведенной продукции 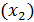и стоимостью основных фондов 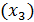, а 4,2% вариация прибыли 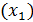объясняется влиянием факторов, которые не вошли в корреляционную модель.

Аналогические рассуждения можно провести и по другим множественным коэффициентам корреляции.

Заканчивая краткое изложение корреляционного анализа количественных признаков, остановимся на двух моментах.

1. Задача научного исследования состоит в отыскании при­чинных зависимостей. Только знание истинных причин явлений позволяет правильно истолковывать наблюдаемые закономерно­сти. Однако корреляция как формальное статистическое понятие сама по себе не вскрывает причинного характера связи. С помо­щью корреляционного анализа нельзя указать, какую перемен­ную принимать в качестве причины, а какую — в качестве след­ствия. Например, рассматривая корреляционную связь между суточной выработкой продукции и величиной основных произ­водственных фондов (см. пример 3.1), изменение последней можно считать одной из причин изменения суточной выработ­ки. Но, с другой стороны, необходимость повышения суточной выработки продукции может повлечь за собой увеличение размера основных производственных фондов. Между урожайностью сель­скохозяйственных культур и погодными условиями (температурой, количеством осадков и т.п.) существует корреляционная связь. Но здесь не возникает сомнений, какая переменная является следствием, а какая — причиной.

Иногда при наличии корреляционной связи ни одна из пере­менных не может рассматриваться причиной другой (например, зависимость между весом и ростом человека). Наконец, воз­можна ложная корреляция (нонсенс-корреляция), т.е. чисто фор­мальная связь между переменными, не находящая никакого объяснения и основанная лишь на количественном соотноше­нии между ними (таких примеров в статистической литературе приводится немало). Поэтому при логических переходах от корре­ляционной связи между переменными к их причинной взаимообу­словленности необходимо глубокое проникновение в сущность ана­лизируемых явлений.

2. Не существует общеупотребительного критерия проверки определяющего требования корреляционного анализа — нормально­сти многомерного распределения переменных. Учитывая свойства теоретической модели, обычно полагают, что отнесение к со­вместному нормальному закону возможно, если частные одно­мерные распределения переменных не противоречат нормаль­ным распределениям (в этом можно убедиться, например, с по­мощью критериев согласия); если совокупность точек корреля­ционного поля частных двумерных распределений имеет вид более или менее вытянутого «облака» с выраженной линейной тенденцией.