Оценки линейного уравнения множественной регрессии

Не требуя нормальный закон распределения вектора 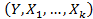, мы должны оценивать функцию 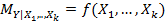, не обязательно линейную. Неизвестная функция, возможно задается сложным аналитическим выражением, но на практике подбирают “хорошую” аппроксимацию для из некоторого параметрического класса функций (β - вектор неизвестных параметров), удобных в вычислительном плане при оценке параметров и т.д.

Возьмем в качестве аппроксимирующей функции линейную функцию

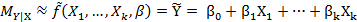
или в векторной форме

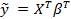
где ,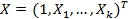

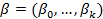
Для оценки линейной функции (уравнения) множественной регрессии построим математическую модель, получим оценки коэффициентов β, изучим свойства оценок уравнения и отдельных коэффициентов.