2015-05-18
2096
Предположим, что для оценки уравнения регрессии взята выборка объемом n. Результаты наблюдений над результативным признаком представлены вектором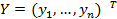 
и матрицей Х типа объект-свойство наблюденных значений признаков 
:
X =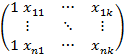 
здесь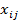 
– значение j-го признака на i-м объекте наблюдения; столбец из "1" можно считать столбцом "наблюденных" значений для признака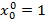 
Очевидно, что, подставляя в правую часть наблюденные значение объясняющих переменных для объекта наблюдение Оi, а в левую часть наблюденное значение результативного признака мы сможем их уравновесить величиной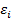 
- регрессионным остатком, характеризующей расхождение между наблюденным значением 
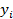и "осредненным" значением 
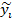- то есть значением линейной функции регрессии:
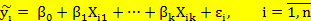
или, если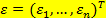 
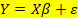
Система линейных уравнений называется линейной моделью множественной регрессии (ЛММР).
Отметим, что наличие регрессионных остатков в (ЛММР) объясняется вариацией результативного признака относительно "среднего значения" при данных значениях объясняющих переменных, что в свою очередь можно объяснить влиянием на результативный признак ряда неучтенных факторов-признаков.
Будем предполагать, что
1) 
– детерминированные переменные;
2) ранг матрицы Х равен "к+1" – среди признаков нет линейно зависимых;
3) 
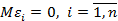- нет систематических ошибок в измерении у;
4) 
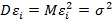- гомоскедастичность регрессионных остатков (равноточные измерения);
5) 
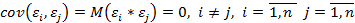- условие некоррелированных регрессионных остатков.
Условия 4 – 5 можно заменить одним условием в векторной форме
4')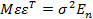 
Условия (1–5) известны как условия Гаусса – Маркова. ЛММР, удовлетворяющая требованиям (1–5), называется классической ЛММР (КЛММР)
