Линейная регрессия: смысл и оценка параметров

Линейная регрессия находит широкое применение в экономет­рике в виде четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида

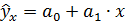или 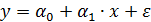. (4.6)

Уравнение вида 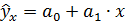позволяет по заданным значени­ям фактора х иметь теоретические значения результативного признака, подставляя в него фактические значения фактора x. На графике теоретические значения представляют линию регрессии (рис. 4.2).

Рис. 4.2. Графическая оценка параметров линейной регрессии

Построение линейной регрессии сводится к оценке ее пара­метров 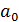и 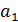.Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию (см. рис. 4.2). Далее по графику можно опреде­лить значения параметров. Параметр 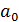определим как точку пе­ресечения линии регрессии с осью 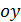,а параметр 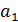оценим, исхо­дя из угла наклона линии регрессии, как 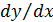,где 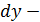прираще­ние результата у, a 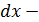приращение фактора х, т. е.

.

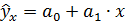Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров 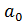и 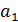,при которых сумма квадратов отклонений фактических значений ре­зультативного признака (у) от расчетных (теоретических) 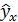ми­нимальна:

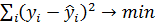. (4.7)

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:

,

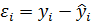cследовательно,

.

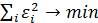Чтобы найти минимум функции (4.7), надо вычислить част­ные производные по каждому из параметров а и b и приравнять их к нулю.

Обозначим 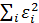через S, тогда:

;

;

.

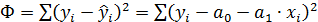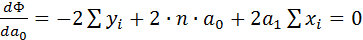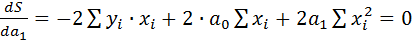Преобразуя эту систему, получим следующую систему нор­мальных уравнений для оценки параметров 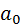и :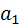

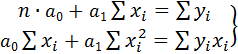. (4.8)

Решая систему нормальных уравнений (4.8) либо методом последовательного исключения переменных, либо методом оп­ределителей, найдем числовые значения искомых параметров 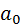и 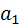. Можно воспользоваться следующими готовыми формулами:

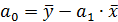. (4.9)

Формула (4.9) получена из первого уравнения системы (4.8), если все его члены разделить на п.

,

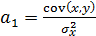где 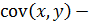ковариация признаков;

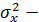дисперсия признака x.

Ввиду того, что 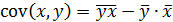, ,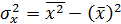получим следующую формулу расчета оценки параметра b:

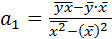. (4.10)

Параметр 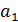называется коэффициентом регрессии. Его вели­чина показывает среднее изменение результата с изменением фактора на одну единицу. Так, если в функции издержек 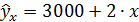(у — издержки (тыс. руб.), х — количество единиц продукции). То, следовательно, с увеличением объема продукции (х) на 1 ед. издержки производства возрастают в среднем на 2 тыс. руб., т. е. дополнительный прирост продукции на 1 ед. потребует увеличения затрат в среднем на 2 тыс. руб.

Возможность четкой экономической интерпретации коэф­фициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследова­ниях.

Формально 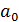— значение у при х = 0. Если признак-фактор 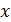не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена 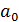не имеет смысла. Параметр 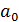может не иметь экономического содержания. Попытки экономически интерпретировать параметр а могут привести к абсурду, особен­но при 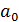< 0.

Интерпретировать можно лишь знак при параметре 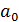. Если 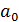> 0, то относительное изменение результата происходит мед­леннее, чем изменение фактора. Иными словами, вариация ре­зультата меньше вариации фактора — коэффициент вариации по фактору х выше коэффициента вариации для результата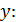 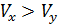.Для доказательства данного положения сравним относи­тельные изменения фактора х и результата у:

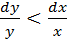или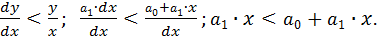

Откуда 0 < .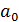

Предположим по группе предприятий, выпускающих один и тот же вид продукции, рассматривается функция издержек: 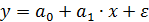.Информация, необходимая для расчета оценок параметров 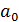и 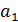,представлена в табл. 4.1.

Таблица 4.1

Расчетная таблица

№ предприятия	Выпуск продукции, тыс. ед. (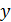)	Затраты на производство, млн руб. (y)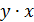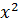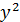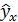
						31,1
						67,9
						141,6
						104,7
						178,4
						104,7
						141,6
Итого						770,0

Система нормальных уравнений будет иметь вид

.

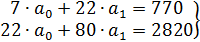Решая ее, получим:

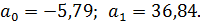
Запишем уравнение регрессии:

.

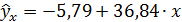Подставив в уравнение значения x, найдем теоретические значения у, (см. последнюю графу табл. 4.1).

В данном случае величина параметра а не имеет экономичес­кого смысла.

В рассматриваемом примере имеем:

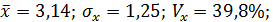
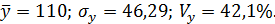
То, что а< О, соответствует опережению изменения результа­та над изменением фактора: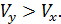

Парная линейная регрессия используется в эконометрике не­редко при изучении функции потребления:

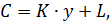
где потребление;

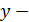доход;

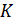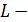и параметри функции.

Данное уравнение линейной регрессии используется обычно в увязке с балансовым равенством:

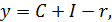
где 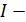размер инвестиций;

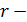сбережения.

Для простоты предположим, что доход расходуется на пот­ребление и инвестиции. Таким образом, рассматривается систе­ма уравнений

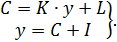
Наличие в данной системе балансового равенства накладыва­ет ограничение на величину коэффициента регрессии, которая не может быть больше единицы, т. е. .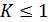

Предположим, что функция потребления составила:

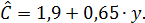
Коэффициент регрессии характеризует склонность к потреб­лению. Он показывает, что из каждой тысячи дохода на потреб­ление расходуется в среднем 650 руб., а 350 руб. инвестируются. Если рассчитать регрессию размера инвестиций от дохода, т. е. 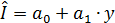,то уравнение регрессии составит: 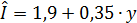.Это уравнение можно и не определять, ибо оно выводится из функции потребления. Коэффициенты регрессии этих двух урав­нений связаны равенством: 0,65 +0,35 = 1.

Если коэффициент регрессии оказывается больше 1, то 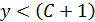, т. е. на потребление расходуются не только доходы, но и сбережения.

Коэффициент регрессии в функции потребления использует­ся для расчета мультипликатора:

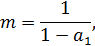
где 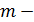мультипликатор;

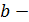коэффициент регрессии в функции потребления.

В нашем примере 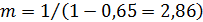. Это означает, что до­полнительные вложения в размере 1 тыс. руб. на длительный срок приведут при прочих равных условиях к дополнительному доходу в 2,86 тыс. руб.