Метод наименьших квадратов для модели множественной линейной регрессии

Для модели множественной линейной регрессии принцип наименьших квадратов состоит в оценке коэффициентов регрессии из условия минимума суммы квадратов остатков. Оцененное уравнение множественной линейной регрессии имеет вид:

Y^=b1x1+b2x2+…+bkxk (1)

Запишем для весх наблюдений:

Y^i=b1xi1+b2xi2+…+bkxik, i=1n

Их также можно записать в матричной форме:Y^=Xb (2)

Где столбцы Y^=(y^1,Y^2,…,y^n)`, b=(b1,b2,…,bk)`.

Определим столбец остатков-отклонений фактических значений yi, зависимой переменной от ее значений y^i, вычисленных по оцененному уравнению регрессии(2):

E=y-y^=y-Xb, e=(e1,e2,….,en)`.

Метод наименьших квадратов заключается в определении коэффициентов оцененного уравнения (2) из условия минимума суммы квадратов остатков:

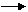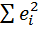e`e= min

На основе св-в операций над матрицами можем записать:

e`e=(y-Xb)`(y-Xb)=(y`-b`X`)(y-Xb)=y`y-b`X`y+b`X`Xb

Это выражение зависит от вектора b и достигает минимума, если его производная по b равна нулевому вектору, т.е

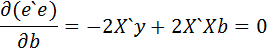
Если столбцы матрицы X` линейно независимы, то существует обратная матрица 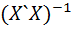X`y (3)

Он также обозначается через 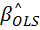. В случае парной линейной регрессии отсюда можно получить оценки коэффиц-ов. Отметим след-ее св-во метода наименьших квадратов. Вектор остатков е ортогенален столбцами матрицы Х. действительно, X`e=X`(y-Xb)=X`y-X`X(X`X)^-1X`y=X`y-X`y=0

В разложении y=y^+e первое слагаемое выражается через векторы-столбцы матрицы Х, а второе слагаемое е от них не зависит. Если модель осдержит постоянный член, то первый столбец матрицы Х состоит из единиц. Значит сумма компонент вектора е в этом случае равна нулю. Тогда и среднее 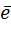=0.

15.Геометрическая интерпретация метода наименьших квадратов.
Рассмотрим геометрическую интерпретацию метода наименьших квадратов. Представим у,х1,…, Хк как векторы в R^N. Эти векторы линейно независимы(в противном случае нет смысла ставить задачу об оценке параметров), т.е. образуют (к+1)- мерное пространство П.По предположению теоремы Гаусса-Маркова, векторы х1,…,хк также линейно независимы и порождают в пространстве П к-мерное подпространство π. Вектор 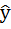=Х 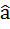0 ортогональная проекция вектора у а подпространство π. Соответственно, е=у 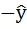-вектор, ортогональный подпространству π. Следовательно, функционал 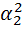=е^Те равен квадрату расстояния между у и π.
Квадрат этого расстояния может быть вычислен с использованием определителя Грама 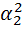= 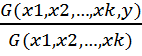, где 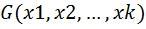- определитель Грама системы векторов х1,х2,…,хк.