Важной задачей регрессионного анализа состоит в построении прогнозов зависимой переменной в зависимости для выбранных значений объясняющей переменной. Значение зависимой переменной при значении х объясняющей переменной должно удовлетворять уравнению 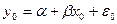 , где ɛ0 реализация случайного члена.
, где ɛ0 реализация случайного члена.
Допустим модели парной линейной регрессии построено ур-ие y=a+bx. Коэффициенты а, б, предполагаются значимыми. Возможен прогноз двух типов. Мат ожидание значения зависимой переменной при x=x0 равно Е(y|x0)= α+ βx0. согласно теореме гаусса-Маркова прогнозом этой величины служит 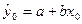 .
.
Возможны два подхода: первый-насколько прогнозное значение может отклонится от условного мат ожидания Е(у|х0). Второй –насколько прогнозное значение у0 зависимой переменной может отклониться от ее прогнозного значения.
1. доверительный интервал для ожидаемого значения зависимой переменной. Основой для построения доверительного интервала явл-ся соотношение 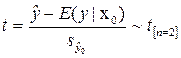 , где оценка
, где оценка 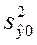 дисперсия прогнозного значения
дисперсия прогнозного значения 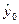 зависимой переменной определяется выражением
зависимой переменной определяется выражением
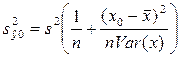 ,
, 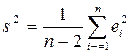 .
.
Для выбранного уровня значимости 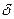 определяется критическое значение
определяется критическое значение 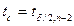 статистики Стьюдента с n-2 степенями свободы. Ответ на вопрос о точности прогноза лается в форме доверительного интервала ожидаемого значения зависимой переменной
статистики Стьюдента с n-2 степенями свободы. Ответ на вопрос о точности прогноза лается в форме доверительного интервала ожидаемого значения зависимой переменной
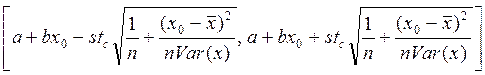
Где s стандартная ошибка случайного члена модели.
2) Доверительный интервал для индивидуального значения зависимой переменной. В этом случае распределение Стьюдента имеет величина
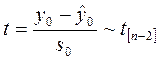 .
.
Построение доверительного интервала сводится к вычислению 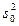 -оценки дисперсии var(e0)=
-оценки дисперсии var(e0)= 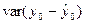 отклонение значения
отклонение значения 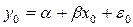 зависимой переменной от ее прогнозного значения. Она равна
зависимой переменной от ее прогнозного значения. Она равна
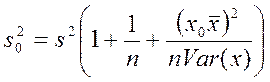
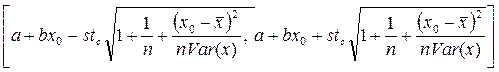
Здесь также 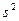 - оценка дисперсии случайного члена, а tc- критическое значение распределения Стьюдента с n-2 степенями свободы.
- оценка дисперсии случайного члена, а tc- критическое значение распределения Стьюдента с n-2 степенями свободы.
 2015-05-18
2015-05-18 555
555








