Пусть нам задана полная система ортонормированных функций одной переменной 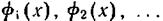 на интервале
на интервале 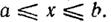 В таком случае полную систему ортонормированных функций двух переменных
В таком случае полную систему ортонормированных функций двух переменных 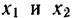 можно построить следующим образом:
можно построить следующим образом:
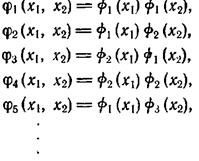 (2.7.10)
(2.7.10)
Отметим, что использованное выше правило построения сводится просто к выбору пар функций из множества функций одной переменной и перемножению их после соответствующей подстановки переменных x1,x2.
Способ распространения описанной процедуры на общий случай п переменных очевиден. Здесь требуется только составлять группы произведений из п функций одной переменной, подставляя соответственно переменные 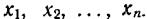 Если исходные функции ортонормированны в интервале
Если исходные функции ортонормированны в интервале 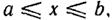 то полученные в результате реализации этой процедуры функции п переменных
то полученные в результате реализации этой процедуры функции п переменных 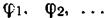 ортонормированны на гиперкубе
ортонормированны на гиперкубе
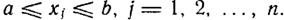 В частности, множество функций п переменных при
В частности, множество функций п переменных при 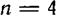 строится следующим образом:
строится следующим образом:
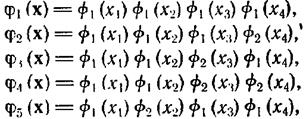 (2.7.13)
(2.7.13)
где, как и выше, 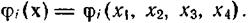
 2015-05-18
2015-05-18 530
530








