Поста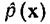новка задачи. Пусть — оценка плотности распределения 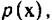при-

Пусть — оценка плотности распределения при-

чем, как и раньше, под 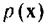подразумевается .

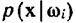Необходимо найти такую оценку, которая обеспечила бы минимиза­цию среднеквадратичной ошибки (интегрального квадратичного показателя качества), определяемой как

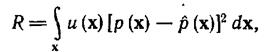(4.6.47)

где 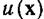— весовая функция.

Воспользуемся разложением оценки 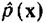в ряд

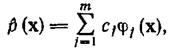
где 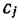—коэффициенты, подлежащие определению, а —

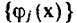множество заданных базисных функций.

Подстановка (4.6.48) в соотношение (4.6.47) дает

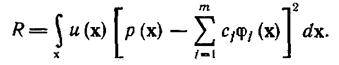(4.6.49)

Требуется найти такие коэффициенты 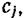которые обеспечат

минимизацию интеграла вероятности ошибки R. Необходимое условие минимальности интеграла вероятности ошибки R за­ключается в том, что

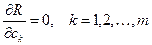(4.6.50)

Взяв частную производную, получим

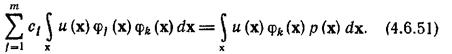
Взглянув на правую часть уравнения (4.6.51), нетрудно убе­диться в том, что она по определению равна математическому ожиданию функции 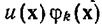. В соответствии с нашим предыдущим анализом математическое ожидание можно аппрокси­мировать выборочным средним, т. е.

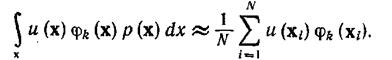(4.6.52)

Подстановка этой аппроксимирующей оценки в уравнение (4.6.51) дает

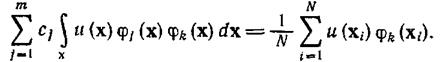(4.6.53)

Если базисные функции 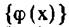выбраны таким образом, что

они ортогональны весовой функции 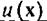, то из определения

ортогональности следует

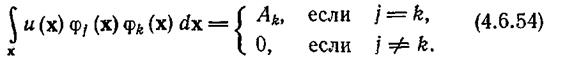
Подстановка (4.6.54) в уравнение (4.6.53) приводит к следую­щему соотношению, позволяющему вычислить искомые коэф­фициенты:

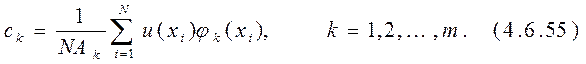
Если базисные функции 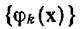ортонормированны, то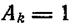

для всех 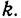Кроме того, поскольку члены 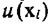не зависят от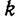

и, следовательно, для всех коэффициентов одинаковы, то их можно исключить из аппроксимирующего выражения без вся­кого ущерба для классификационной мощности коэффициентов. В таком случае

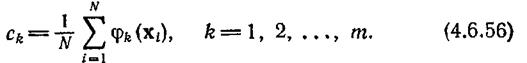
После того как коэффициенты определены, с помощью форму­лы (4.6.48) формируется оценка плотности распределения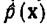

Для того чтобы применение выражений (4.6.48) и (4.6.55) или (4.6.56) приводило к успеху, необходимо иметь в виду два существенных обстоятельства. Во-первых, следует полностью отдавать себе отчет в том, что качество аппроксимации с по­мощью выбранной системы базисных функций зависит от числа m членов разложения. Поскольку, по всей вероятности, вид плотности распределения 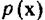нам не известен, оценить

качество аппроксимации 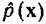при помощи непосредственного

сравнения невозможно. С другой стороны, так как оценка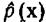

отыскивается для того, чтобы построить байесовский классифи­катор, то заботиться следует только о качестве распознавания, доступном этому классификатору. Последнее можно установить непосредственно в эксперименте с обучающей выборкой. Если при некоторой оценке 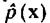качество классификации оказывается неудовлетворительным, следует попробовать увеличить число базисных функций и посмотреть, приводит ли улучшение качества оценки 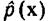к улучшению качества классификатора.

Эту процедуру можно продолжать вплоть до наступления «на­сыщения» (когда введение дополнительных членов не произво­дит никакого либо очень малый эффект) или до тех пор, пока число членов не начнет превосходить допустимую величину.

Вторым важным моментом является выбор базисных функ­ций. Так, например, если плотность распределения 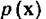имеет синусоидальный характер, а для разложения оценки 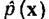ис­пользован степенной ряд, то очевидно, что число членов будет значительно больше, чем при выборе синусоидальных базисных функций. Естественно, при отсутствии априорных сведений о характере плотности распределения 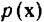базисные функции в первую очередь должны выбираться исходя из простоты реали­зации. 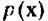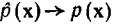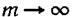Все, что можно было бы сказать об общих правилах выбора базисных функций, сводится к тому, что при выполне­нии условия линейной независимости и некоторых других не очень жестких ограничений на вид плотности распределения можно доказать сходимость при и 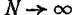. Отметим, что ортогональность является частным слу­чаем линейной независимости.