Многочлены Лежандра

Ортогональные полиномиальные функции Лежандра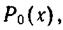

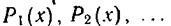можно получить, воспользовавшись следующим рекуррентным соотношением:

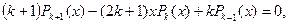
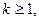(2.7.14)

где 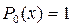и 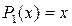Эти функции ортогональны в интервале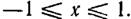

Приведем несколько первых многочленов Лежандра:

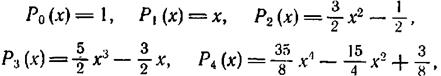
где функци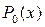и и 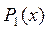заданы, а функци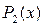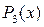и , и 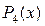получены по формуле (2.7.14). Эти функции ортогональны относительно весовой функции

и(х)= 1.

Многочлены Лагерра

Для получения многочленов Лагерра можно воспользоваться рекуррентным соотношением

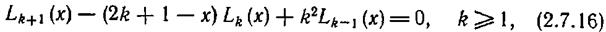
где 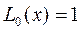^{и 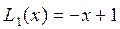.} Эти многочлены ортогональны

относительно весовой функции 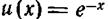в интервале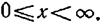

Приведем несколько первых многочленов Лагерра:

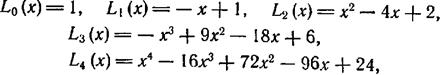
где функции 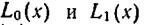заданы, а остальные получены по формуле (2.7.16).