Функции двух переменных. Основные понятия

Учебные вопросы

Учебные вопросы и расчет времени

I. Введение _________________________________________ 5 мин

II. Основная часть ___________________________________ 80 мин

1. Функции двух переменных. Основные понятия __________ 25 мин

2. Предел и непрерывность функции двух переменных ______ 25 мин

3. Частные производные. Касательная плоскость и нормаль

к поверхности ______________________________________ 30 мин

III. Заключение _______________________________________ 5 мин

Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.

Будем рассматривать функции двух переменных, так как все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. Кроме того, для функций двух переменных можно дать наглядную геометрическую интерпретацию.

Пусть задано множество D упорядоченных пар чисел 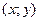. Соответствие f, которое каждой паре чисел 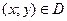сопоставляет одно и только одно число 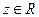, называется функцией двух переменных, определенной на множестве 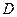со значениями в R, и записывается в виде 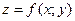или 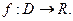При этом x и y называются независимыми переменными (аргументами), а z – зависимой переменной (функцией).

Множество 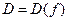называется областью определения функции. Множество значений, принимаемых z в области определения, называется областью изменения этой функции, обозначается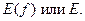

Примером функции двух переменных может служить площадь S прямоугольника со сторонами, длины которых равны x и y: S = xy. Областью определения этой функции является множество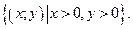

Функцию 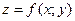, где 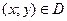можно понимать (рассматривать) как функцию точки 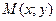координатной плоскости 0ху. В частности, областью определения может быть вся плоскость или её часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границе называется замкнутой, обозначается 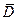. Примером замкнутой области является круг с окружностью.

Значение функции 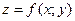в точке 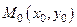обозначают 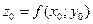или 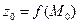и называют частным значением функции.

Функция двух независимых переменных допускает геометрическое истолкование. Каждой точке 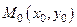области D в системе координат 0xyz соответствует точка 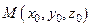, где 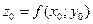– аппликата точки М. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию 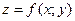. Например, функция 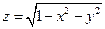имеет областью определения круг 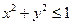и изображается верхней полусферой с центром в точке 0(0; 0;0) и радиусом R = 1 см (рис. 1).

z

1

1 y

x 1

Рис. 1

Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило, аналитическим способом: когда функция задается с помощью формулы.