Нелинейная регрессия. 1.4.1. Виды нелинейной регрессии

1.4.1. Виды нелинейной регрессии.
Оценка параметров нелинейной регрессии

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций, например равносторонней гиперболы: 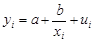; параболы второй степени: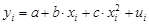 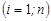и др.

Различают два класса нелинейных регрессий:

· относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

· по оцениваемым параметрам.

Нелинейные регрессии по включаемым в нее объясняющим переменным, но линейные по оцениваемым параметрам

Данный класс нелинейных регрессий включает уравнения, в которых у линейно связан с параметрами. Примером могут служить следующие функции.

Полиномы разных степеней – 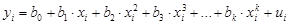– (полином k -й степени).

Равносторонняя гипербола – .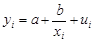

Оценка параметров регрессий нелинейных по объясняющим переменным. При этом используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми «линейными» переменными и сведение нелинейной регрессии к линейной. К новой «преобразованной» регрессии может быть применен обычный метод наименьших квадратов (МНК).

Рассмотрим применение данного подхода к параболе второй степени: 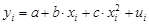. Заменяя переменную х² на z, получим двухфакторное уравнение линейной регрессии: 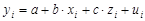, для оценки параметров которого используется обычный МНК.

Соответственно, для полинома k -го порядка ,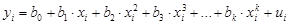

при замене: 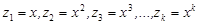получим

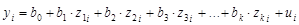
Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез.

Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях — полином третьего порядка. Ограничение в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, менее однородна совокупность по результативному признаку.

Парабола второй степени (рис. 1.6) целесообразна к применению, если для определенного интервала значений фактора меняется характер связи с результатом: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака:

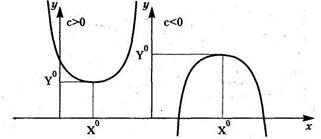
Рис. 1.6. Параболическая зависимость

Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второй степени становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.

Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу: 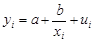. Она может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции.

Для оценки параметров равносторонней гиперболы используется тот же подход «замены переменных»: заменив 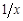на z, получим линейное уравнение регрессии: 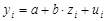, для которого может быть применен обычный МНК.

При b > 0 имеем обратную зависимость, которая при х ® µ характеризуется нижней асимптотой, т. е. минимальным предельным значением у, оценкой которого служит параметр а (рис. 1.7, а).

При b < 0 имеем медленно повышающуюся функцию с верхней асимптотой при х ® µ, т. е. максимальным предельным уровнем у, оценкой которого служит параметр а (рис. 1.7, б).

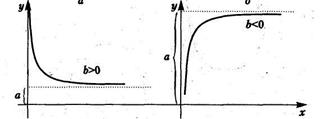
Рис. 1.7. Зависимость в виде равносторонней гиперболы

Регрессии нелинейные по оцениваемым параметрам. К данному классу регрессий относятся уравнения, в которых у нелинейно связан с параметрами. Примером таких нелинейных регрессий являются функции:

· степенная – ;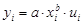

· показательная – ;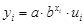

· экспоненциальная – .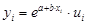

Данный класс нелинейных моделей подразделяется на два типа:

1) нелинейные модели внутренне линейные;

2) нелинейные модели внутренне нелинейные.

Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду (например, логарифмированием и заменой переменных). Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции.

Примером нелинейной по параметрам регрессии внутренне линейной является степенная функция, которая широко используется в эконометрических исследованиях при изучении спроса от цен:

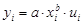
где у – спрашиваемое количество;

х – цена;

u – случайная составляющая.

Данная модель нелинейна относительно оцениваемых параметров, т. к. включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду: 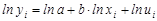. Заменив переменные и параметры, получим линейную регрессию, оценки параметров которой а и b могут быть найдены МНК.

В рассматриваемой выше степенной функции предполагалось, что случайная составляющая u мультипликативно связана с объясняющей переменной х. Если же модель представить в виде 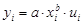, то она становится внутренне нелинейной, т. к. ее невозможно преобразовать к линейному виду.

Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

Применение МНК для оценки параметров нелинейных моделей внутренне линейных. В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. В таких моделях преобразованию подвергается результативный признак у, в отличие от нелинейных моделей 1-го типа, где результативный признак у остается неизменным, а преобразуется факторный признак.

Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия 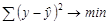, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е. 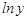, 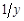. Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений логарифмов:

.

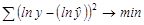Соответственно, если в линейных моделях и моделях, нелинейных по переменным, 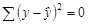, то в моделях, нелинейных по оцениваемым параметрам, 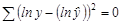, а 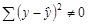. Вследствие этого оценка параметров с помощью МНК для нелинейных моделей, внутренне линейных, оказывается несколько смещенной.

При исследовании взаимосвязей среди функций, использующих 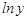, в эконометрике преобладают степенные зависимости – это кривые спроса и предложения, кривые Энгеля, производственные функции, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения выпуска нового вида изделий, а также зависимость валового национального дохода от уровня занятости.

Для оценки параметров степенной функции 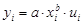применяется МНК к линеаризованному уравнению 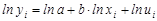, т. е. решается система нормальных уравнений:

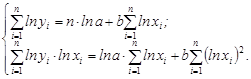
Параметр b определяется непосредственно из системы, а параметр а – косвенным путем после потенцирования величины .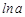

Поскольку параметр а экономически не интерпретируется, то нередко зависимость записывается в виде логарифмически линейной, т. е. как: .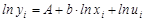

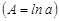В виде степенной функции изучается эластичность не только спроса, но и предложения. При этом обычно в функциях спроса параметр b < 0, а в функциях предложения – b > 0.

В отдельных случаях может использоваться так называемая обратная функция: 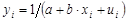, являющаяся разновидностью гиперболы. Но если в равносторонней гиперболе 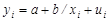, преобразованию подвергается объясняющая переменная 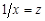и 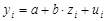, то для получения линейной формы зависимости в обратной модели преобразовывается у: 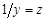. Тогда модель обратной зависимости принимает вид: .

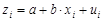Обратная модель является внутренне линейной по параметрам. Требование МНК при этом выполняется для обратных значений результативного признака – 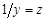, а именно: .

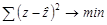Поскольку уравнение обратной функции линейно относительно величин 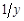, то, если обратные значения 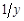имеют экономический смысл, коэффициент регрессии интерпретируется так же, как в линейном уравнении регрессии. Если, например, под у подразумеваются затраты на рубль продукции, а под х – производительность труда (выработка продукции на одного работника), то обратная величина характеризует затратоотдачу, и параметр b имеет экономическое содержание – средний прирост продукции в стоимостном измерении на 1 руб. затрат с ростом производительности труда на единицу своего измерения.