Естественным обобщением линейной регрессии с двумя переменными является многомерная регрессионная модель (multiple regression model) или модель множественной регрессии:
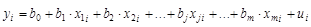
где уi – значение признака-результата (зависимой переменной) для i -го наблюдения;
хji – значение j -го фактора (независимей или объясняющей переменной) (j = 1;т) для i -го наблюдения;
иг – случайная составляющая результативного признака для i -го наблюдения;
bо – свободный член, который формально показывает среднее значение у при х1 = х2 =... = хт = 0;
bj – коэффициент «чистой» регрессии при j-m факторе (j=1,m). Он характеризует среднее изменение признака-результата у с изменением соответствующего фактора хj. на единицу, при условии, что прочие факторы модели не изменяются и фиксированы на средних уровнях.
Обычно для многомерной регрессионной модели делаются следующие предпосылки.
1. 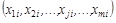 – детерминированные (нестохастические) переменные.
– детерминированные (нестохастические) переменные.
2. 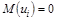 , (i = 1, n) – математическое ожидание случайной составляющей равно 0 в любом наблюдении.
, (i = 1, n) – математическое ожидание случайной составляющей равно 0 в любом наблюдении.
3. 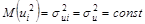 , (i = 1, n) – теоретическая дисперсия случайной составляющей; постоянна для всех наблюдений.
, (i = 1, n) – теоретическая дисперсия случайной составляющей; постоянна для всех наблюдений.
4. 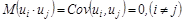 – отсутствие систематической связи между значениями случайной составляющей в любых двух наблюдениях.
– отсутствие систематической связи между значениями случайной составляющей в любых двух наблюдениях.
5. Часто добавляется условие: 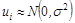 , т. е.
, т. е. 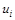 – нормально распределенная случайная величина.
– нормально распределенная случайная величина.
Модель линейной множественной регрессии, для которой выполняются данные предпосылки, называется нормальной линейной регрессионной (Classical Normal Regression model).
В матричной форме нормальная (классическая) регрессионная, модель имеет вид:
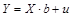 ,
,
где Y – случайный вектор-столбец размерности (n ´1) наблюдаемых значений результативного признака;
X – матрица размерности (n ´(m +1)) наблюдаемых значений факторных признаков. Добавление 1 к общему числу факторов т учитывает свободный член b0 в уравнении регрессии. Значения фактора х0 для свободного члена принято считать равным единице;
b – вектор-столбец размерности ((т +1)´1) неизвестных, подлежащих оценке параметров модели (коэффициентов регрессии);
и – случайный вектор-столбец размерности (n´1) ошибок наблюдений.
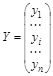
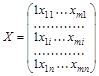
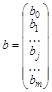
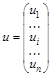
Предпосылки данной модели:
1) 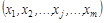 – детерминированные (нестохастические) переменные, т. е. ранг матрицы X равен т+1<n;
– детерминированные (нестохастические) переменные, т. е. ранг матрицы X равен т+1<n;
2) 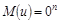 ;
;
3,4) ковариационная матрица должна иметь вид:
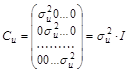 ,
,
где 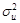 – дисперсия случайной составляющей;
– дисперсия случайной составляющей;
I – единичная матрица размером п´п;
5) 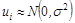 .
.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. Если не обходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов).
2. Каждый фактор должен быть достаточно тесно связан с результатом (т. е. коэффициент парной линейной корреляции между фактором и результатом должен существенно отличаться от нуля).
3. Факторы не должны сильно коррелировать друг с другом, тем более находиться в строгой функциональной связи (т. е. они не должны быть интеркоррелированны).
2.1.2. Традиционный метод наименьших квадратов
для многомерной регрессии (OLS)
Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных коэффициентов регрессии 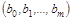 модели или вектора
модели или вектора 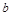 .
.
Оценка параметров многомерной модели, как и в случае парной регрессии, осуществляется обычно традиционным методом наименьших квадратов (МНК). Согласно данному методу, в качестве оценки вектора 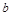 принимают вектор
принимают вектор 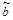 , который минимизирует сумму квадратов отклонений наблюдаемых значений yi от рассчитанных по модели
, который минимизирует сумму квадратов отклонений наблюдаемых значений yi от рассчитанных по модели 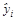 .
.
В матричной форме функционал S будет записан так:
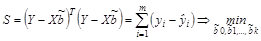
МНК-оценки в матричной форме находят по формулам:
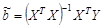 , где
, где 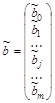 .
.
Оценим с помощью МНК параметры линейной двухфакторной модели: 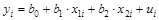 , i=1; n. Для этого минимизируем функционал:
, i=1; n. Для этого минимизируем функционал:
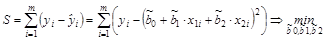
Функционал S является функцией трех переменных 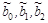 . Чтобы найти экстремум функции нескольких переменных, нужно взять ее частные производные по этим переменным и приравнять их нулю:
. Чтобы найти экстремум функции нескольких переменных, нужно взять ее частные производные по этим переменным и приравнять их нулю:
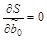 ,
, 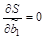 ,
, 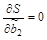 .
.
Получим следующую систему нормальных линейных уравнений:
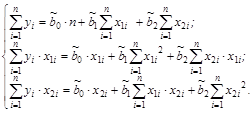
Параметры этой системы могут быть найдены, например, методом К. Гаусса, либо методом итераций.
Рассмотрим пример. Для данных табл. 2.1 найдем МНК-оценки параметров линейного двухфакторного уравнения регрессии: 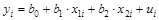 .
.
Расчет необходимых сумм для системы нормальных линейных уравнений сведем в табл. 2.1.
Таблица 2.1
| i | у – заработная плата, $ | х1 –возраст, лёт | х2 – выработка, шт./смену | yx1 | yx2 | x12 | x22 | x1x2 |
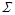 |
Тогда система нормальных линейных уравнений будет иметь вид:
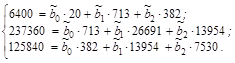
Решив систему, найдем значения 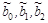 :
:
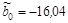 ;
; 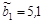 ;
; 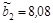 .
.
Найдем МНК-оценки для нашего примера матричным способом.
Воспользовавшись правилами умножения матриц будем иметь:
ХТХ=
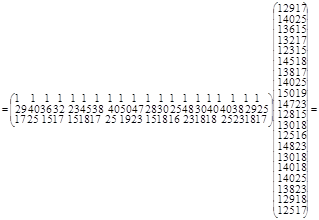
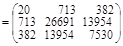 .
.
ХТХ=
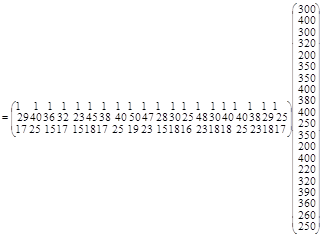
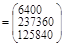
Найдем обратную матрицу.
Матрицей, обратной к матрице А, называется матрица А-1 такая, что АА-1 =I (I – единичная матрица).
Обозначим aij элементы матрицы А-1. Тогда 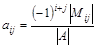 , где Mij – матрица, получающаяся из А вычеркиванием i -й строки и j -го столбца. Для нашего примера:
, где Mij – матрица, получающаяся из А вычеркиванием i -й строки и j -го столбца. Для нашего примера:
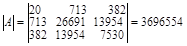 ;
;
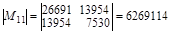 ;
;
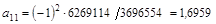 и т.д.
и т.д.
В результате получим:
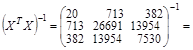
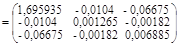
Тогда вектор оценок коэффициентов регрессии равен:
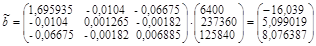
То есть 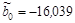 ;
; 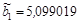 ;
; 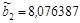 (оценки такие же, что и найденные 1-м способом).
(оценки такие же, что и найденные 1-м способом).
Кроме того, для линейной множественной регрессии существует другой способ оценки параметров – через 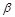 -коэффициенты (параметры уравнения регрессии в стандартных масштабах).
-коэффициенты (параметры уравнения регрессии в стандартных масштабах).
При построении уравнения регрессии в стандартном масштабе все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам:
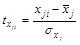 , j=1;m,
, j=1;m,
где xji – значение переменной хj в i -м наблюдении.
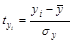 .
.
Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квадратическое отклонение (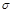 ). Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:
). Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:
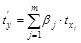 .
.
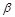 -коэффициенты могут быть оценены с помощью обычного МНК.
-коэффициенты могут быть оценены с помощью обычного МНК.
При этом система нормальных уравнений будет иметь вид:
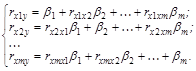
(так как 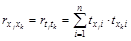 ).
).
Найденные из данной системы 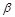 -коэффициенты позволяют определить значения коэффициентов регрессии в естественном масштабе по формулам:
-коэффициенты позволяют определить значения коэффициентов регрессии в естественном масштабе по формулам:
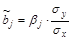 , j=1;m;
, j=1;m; 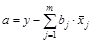 .
.
Найдем 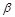 -коэффициенты для нашего примера. Система нормальных линейных уравнений будет иметь вид (воспользуемся данными корреляционной матрицы, рассчитанной в предыдущем вопросе):
-коэффициенты для нашего примера. Система нормальных линейных уравнений будет иметь вид (воспользуемся данными корреляционной матрицы, рассчитанной в предыдущем вопросе):
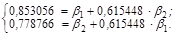
Тогда 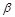 1 = 0,60166,
1 = 0,60166, 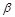 2 = 0,408476.
2 = 0,408476.
Отсюда 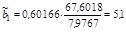 .
. 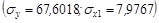 ;
;
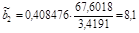
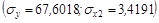 ;
;
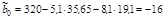
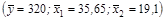
Оцененное уравнение регрессии для нашего примера будет иметь вид: 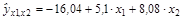 .
.
Дадим интерпретацию параметров данного уравнения.
Параметр 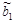 =–5,099019 показывает, что заработная плата рабочего в среднем увеличивается на 5$ при увеличении возраста рабочего на 1 год при условии, что выработка рабочего не меняется и фиксирована на среднем уровне; параметр
=–5,099019 показывает, что заработная плата рабочего в среднем увеличивается на 5$ при увеличении возраста рабочего на 1 год при условии, что выработка рабочего не меняется и фиксирована на среднем уровне; параметр 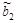 =8,076387 показывает, что заработная плата рабочего в среднем увеличивается на 8$ при увеличении выработки рабочего за смену на 1 штуку при условии, что возраст рабочего не изменился и фиксирован на среднем уровне.
=8,076387 показывает, что заработная плата рабочего в среднем увеличивается на 8$ при увеличении выработки рабочего за смену на 1 штуку при условии, что возраст рабочего не изменился и фиксирован на среднем уровне.
Параметр 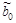 мы не интерпретируем, т. к. в выборке отсутствуют значения признаков x1 и x2, близкие к нулю.
мы не интерпретируем, т. к. в выборке отсутствуют значения признаков x1 и x2, близкие к нулю.
2.1.3. Показатели тесноты связи фактора с результатом. Коэффициенты частной эластичности и стандартизированные коэффициенты регрессии (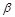 – коэффициенты)
– коэффициенты)
Если факторные признаки различны по своей сущности и/или имеют различные единицы измерения, то коэффициенты регрессии 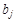 уравнения:
уравнения: 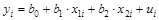 являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат. К таким показателям тесноты связи относят: частные коэффициенты эластичности,
являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат. К таким показателям тесноты связи относят: частные коэффициенты эластичности, 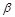 -коэффициенты и другие.
-коэффициенты и другие.
Частные коэффициенты эластичности 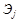 рассчитываются по формуле:
рассчитываются по формуле:
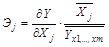
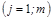 ,
,
где 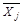 – среднее значение фактора xj;
– среднее значение фактора xj;
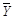 – среднее значение результата у.
– среднее значение результата у.
Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется признак-результат у с увеличением признака-фактора хj на 1 % от своего среднего уровня при фиксированном положении других факторов модели. В случае линейной зависимости 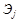 рассчитываются по формуле:
рассчитываются по формуле:
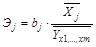 ,
,
где 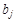 – коэффициент регрессии при j -м факторе.
– коэффициент регрессии при j -м факторе.
Стандартизированные частные коэффициенты регрессии 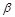 -коэффициенты (
-коэффициенты (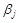 ) показывают, на какую часть своего среднего квадратического отклонения
) показывают, на какую часть своего среднего квадратического отклонения 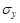 изменится признак-результат у с увеличением соответствующего фактора хj на величину своего среднего квадратического отклонения (
изменится признак-результат у с увеличением соответствующего фактора хj на величину своего среднего квадратического отклонения (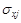 ) при неизменном влиянии прочих факторов модели.
) при неизменном влиянии прочих факторов модели.
Частные коэффициенты эластичности и стандартизованные частные коэффициенты регрессии можно использовать для ранжирования факторов по силе влияния на результат. Чем больше величина 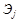 или
или 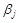 , тем сильнее влияет фактор хj на результат у.
, тем сильнее влияет фактор хj на результат у.
Пример. Рассмотрим ранжирование факторов на примере. Исходные данные были приведены в табл. 2.1. Воспользуемся результатами оценивания регрессии заработной платы рабочих у по возрасту x1 и выработке х2:
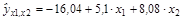 (2.1)
(2.1)
(см. п. 2.1.2).
Частный коэффициент эластичности для фактора «возраст» будет равен: 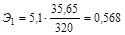
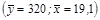 .
.
Частный коэффициент эластичности для фактора «выработка» равен: 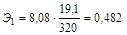
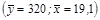 . Так как Э1 > Э2, то фактор «возраст» сильнее влияет на заработную плату рабочего (т. е. вызывает более существенное изменение заработной платы), чем фактор «выработка».
. Так как Э1 > Э2, то фактор «возраст» сильнее влияет на заработную плату рабочего (т. е. вызывает более существенное изменение заработной платы), чем фактор «выработка».
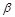 -коэффициенты для данного примера были рассчитаны в п. 2.1.2 и составили, соответственно, для фактора«возраст», (x1):
-коэффициенты для данного примера были рассчитаны в п. 2.1.2 и составили, соответственно, для фактора«возраст», (x1): 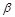 1 = 0,60166, для фактора «выработка» (х2):
1 = 0,60166, для фактора «выработка» (х2): 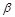 2 = 0,408476. Так как
2 = 0,408476. Так как 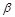 1, >
1, > 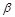 2, то фактор «возраст» сильнее влияет на заработную плату рабочего (т. е. вызывает более существенное изменение заработной платы), чем фактор«выработка».
2, то фактор «возраст» сильнее влияет на заработную плату рабочего (т. е. вызывает более существенное изменение заработной платы), чем фактор«выработка».
По коэффициентам эластичности и
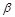 -коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.
-коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.
Коэффициент 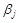 может также интерпретироваться как показатель прямого (непосредственного) влияния j -го фактора хj на результат у. Во множественной регрессии j -й фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т. е. влияет на результат через другие факторы модели). Косвенное влияние измеряется величиной:
может также интерпретироваться как показатель прямого (непосредственного) влияния j -го фактора хj на результат у. Во множественной регрессии j -й фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т. е. влияет на результат через другие факторы модели). Косвенное влияние измеряется величиной: 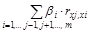 , где m – число факторов в модели. Полное влияние j -го фактора на результат, равное сумме прямого и косвенного влияний, измеряет коэффициент линейной парной корреляции данного фактора и результата –
, где m – число факторов в модели. Полное влияние j -го фактора на результат, равное сумме прямого и косвенного влияний, измеряет коэффициент линейной парной корреляции данного фактора и результата – 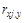 .
.
Так для нашего примера непосредственное влияние фактора «возраст» на результат «заработную плату» в уравнении регрессии (2.1) измеряется 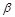 1 и составляет 0,60166; косвенное (опосредованное) влияние данного фактора на результат определяется как:
1 и составляет 0,60166; косвенное (опосредованное) влияние данного фактора на результат определяется как: 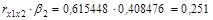 .
.
Непосредственное влияние фактора «выработка» на результат «заработная плата» в уравнении регрессии (3) измеряется 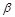 2 и составляет 0,408476. Косвенное влияние данного фактора на результат определяется как:
2 и составляет 0,408476. Косвенное влияние данного фактора на результат определяется как: 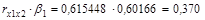 .
.
 2015-05-18
2015-05-18 3831
3831
