Пусть построено уравнение парной регрессии 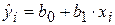 . На основе построенной модели рассчитываются точечные и интервальные прогнозы. Точечный прогноз при
. На основе построенной модели рассчитываются точечные и интервальные прогнозы. Точечный прогноз при 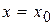 получается путем подстановки значения
получается путем подстановки значения 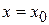 в уравнение регрессии:
в уравнение регрессии:
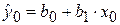 . (1.3.1)
. (1.3.1)
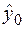 является точечной оценкой условного математического ожидания (среднего значения) переменной
является точечной оценкой условного математического ожидания (среднего значения) переменной 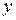 при
при 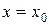 . Чтобы измерить точность полученной оценки и построить доверительный интервал для среднего значения, необходимо найти дисперсию точечной оценки
. Чтобы измерить точность полученной оценки и построить доверительный интервал для среднего значения, необходимо найти дисперсию точечной оценки 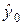 , по которой формируется интервальная оценка.
, по которой формируется интервальная оценка.
Воспользуемся уравнением регрессии (1.1.18):
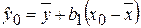 . (1.3.2)
. (1.3.2)
Дисперсия оценки 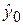 равна сумме дисперсий для независимых слагаемых выражения (1.3.2)
равна сумме дисперсий для независимых слагаемых выражения (1.3.2)
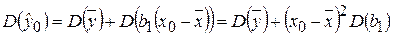 . (1.3.3)
. (1.3.3)
Подставляя в (1.3.3) дисперсию коэффициента регрессии (1.1.21) и дисперсию выборочной средней
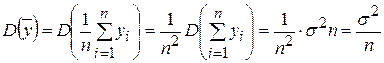 ,
,
получим
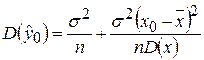 . (1.3.4)
. (1.3.4)
Из формулы видно, что дисперсия предсказания убывает с ростом объема выборки n и она тем больше, чем больше 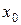 отклоняется от выборочного среднего
отклоняется от выборочного среднего 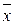 .
.
Заменяя в выражении (1.3.4) неизвестное значение дисперсии 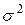 на ее оценку
на ее оценку 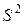 , можно записать формулу для выборочной дисперсии оценки среднего значения в точке
, можно записать формулу для выборочной дисперсии оценки среднего значения в точке 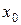
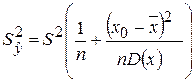 . (1.3.5)
. (1.3.5)
Если предпосылки (1.1.5)-(1.1.8) верны, то можно показать, что статистика 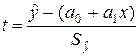 имеет распределение Стьюдента с (n- 2 ) степенями свободы. Используя стандартную процедуру, рассмотренную выше, получим доверительный интервал для функции регрессии
имеет распределение Стьюдента с (n- 2 ) степенями свободы. Используя стандартную процедуру, рассмотренную выше, получим доверительный интервал для функции регрессии
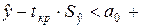
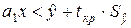 . (1.3.6)
. (1.3.6)
 2015-05-18
2015-05-18 647
647








