2015-05-18
6514
Значения экономических показателей определяются, как правило, влиянием нескольких факторов. В этом случае возникает задача исследования зависимости одной зависимой переменной (результативного признака)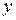 
от нескольких независимых переменных (объясняющих факторов, регрессоров)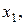 
…, 
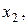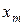, т. е. задача множественной регрессии. Наиболее простой и самой употребляемой является модель множественной линейной регрессии:
,
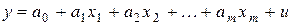или для конкретных наблюдений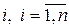 
,
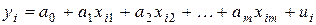, (2.1.1)
где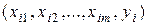 
– выборка объема 
, 
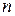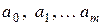– неизвестные параметры модели, подлежащие оцениванию, 
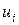– значение случайного возмущения (ошибки) в наблюдении 
.
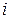Модель (2.1.1) называется классической (нормальной) линейной моделью множественной регрессии (КЛММР), если для нее выполняются условия Гаусса-Маркова 1-5 (п. 1.1) и 6 предпосылка об отсутствии между объясняющими переменными строгой линейной зависимости.
Представим выборочные данные в виде вектора-столбца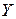 
значений зависимой переменной и матрицы 
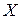значений объясняющих переменных (первый столбец является единичным, так как в уравнении регрессии параметр 
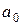умножается на 1):
, 
.
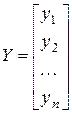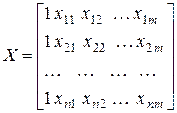Один столбец матрицы X – это вектор значений одной из независимых переменных.
Тогда в матричной форме модель (2.1.1) примет вид:
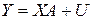, (2.1.2)
где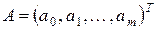 
– вектор-столбец параметров регрессии; 
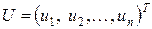– вектор-столбец случайных возмущений.
Поскольку истинные значения параметров по выборке получить невозможно, то задача состоит в нахождении оценок (приближенных значений)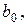 
..., 
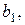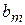неизвестных параметров модели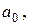 
..., 
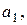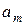по исходным данным , 
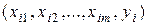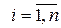. Это означает построение уравнения
,
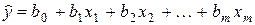которое называется уравнением линейной регрессии. При подстановке в это уравнение значений факторных переменных i -го наблюдения получим величину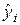 
:
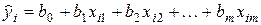, (2.1.3)
которая не будет совпадать с наблюдаемым значением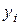 
. Разность между наблюдаемым значением 
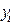и значением, рассчитанным по уравнению регрессии, называется остатком в наблюдении i и обозначается 
:
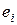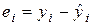. (2.1.4)
Используя соотношение (2.1.4), наблюдаемые значения 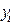можно представить как
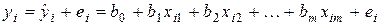. (2.1.5)
Представим коэффициенты уравнения регрессии в виде вектора-столбца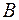 
, а остатки наблюдений – в виде вектора-столбца E: 
; 
.
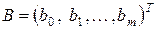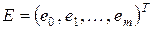Используя введенные обозначения, соотношение (2.1.5) можно записать в матричной форме:
. (2.1.6)
Предпосылки – условия Гаусса – Маркова – также можно записать в матричной форме.
1. Математическое ожидание вектора возмущения равно нулю: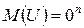 
.
Условия 2 и 3 можно объединить в одно, определяющее вид ковариационной матрицы возмущений: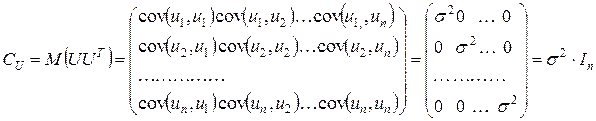 
,
где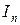 
– единичная матрица размером 
.
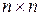4. 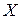– детерминированная матрица.
5. 
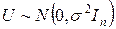– нормально распределенный случайный вектор с нулевым математическим ожиданием и ковариационной матрицей 
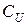. 6. Векторы объясняющих переменных (столбцы матрицы X) линейно независимы (ни один из них не может быть представлен в виде линейной комбинации других). Другими словами, ранг матрицы X равен числу ее столбцов m+1.
